Autor: Mauro Benito Montoya Arenas (mauro2017pre@gmail.com) 

LABORATORIO N°5: “SINTESIS AUTOMATICA Y SIMULACION DEL LAYOUT”

RESUMEN:

En este laboratorio hemos vuelto a desarrollar los circuitos del laboratorio 4, pero esta vez lo realizamos en el Software DSCH. Pero este software no simula circuitos de lógica dinámica, por eso, fue necesario exportarlo a Microwind con un archivo verilog. Después, realizamos una breve explicación de los circuitos comparador y multiplicador. Además, realizamos su simulación y prueba en DSCH, para después exportarlos a Microwind. En todos los circuitos hechos en DSCH especificamos sus características (frecuencia máxima de operación y área ocupada).

INTRODUCCION:

El programa DSCH es un editor y simulador lógico diseñado por un grupo de investigación bajo la dirección de E.Sicard, profesor del INSA de Toulouse. DSCH se utiliza para validar la arquitectura del circuito lógico antes de que se inicie el diseño microelectrónico. DSCH proporciona un entorno fácil de usar para el diseño de lógica jerárquica y una simulación rápida con análisis de retardo, que permite el diseño y validación de estructuras lógicas complejas.

OBJETIVOS:

        - Hacer los circuitos en DSCH y exportarlos a Microwind.

- Aprender el funcionamiento de los comparadores y multiplicadores.

- Detallar las características de los distintos layouts creados de la importación de DSCH a             Microwind.

TEMA PROPUESTO:

Laboratorio N°5: “Síntesis automática y simulación del layout”

BASES TEORICAS:

Marco Teórico:

Lógica CMOS dinámica de precarga y evaluación (PE Logic)

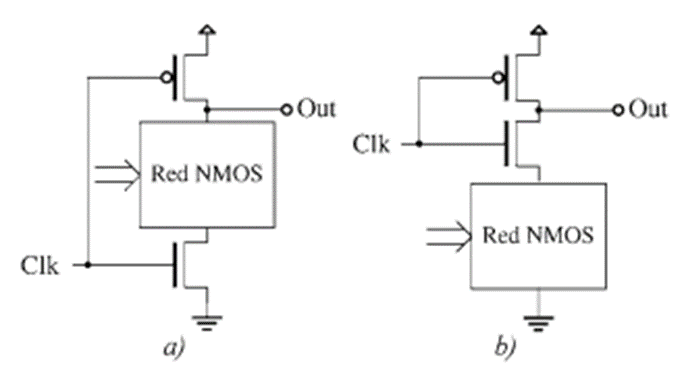
En la figura de abajo, se muestra la estructura de una lógica dinámica básica denominada de Precarga y Evaluación (PE Logic). Dicha lógica está formada por una red de transistores NMOS (encargada de realizar la función lógica), cuya salida (que es dinámica) se precarga a VDD mediante un transistor PMOS de pull-up cuando la señal de reloj vale ‘0’ (en ese momento el transistor NMOS que conecta la red a GND está en corte). Esa es la fase de precarga de la salida. 

Figura 1. Estructura lógica dinámica de precarga y evaluación

Una vez las entradas han tomado el valor a evaluar, el reloj φ se conmuta a ‘1’, con lo que el PMOS entra en corte y el NMOS en conducción. Si el vector de entrada es tal que la función lógica implementada vale cero la red NMOS presenta conducción, con lo que la salida se descargará a través de dicha red y del transistor NMOS controlado por φ. Si no es así y la función vale ‘1’, la red no presentará conectividad, con lo que la salida permanecerá en alta impedancia recordando el valor precargado, ‘1’. Esta segunda fase es la de evaluación. Nótese que el transistor de evaluación puede estar situado tanto conectando la red NMOS a GND como a la salida, como se muestra en la figura siguiente. Esta lógica tiene el inconveniente de que las entradas sólo pueden variar durante la fase de precarga, ya que si lo hacen durante la de evaluación podría dar lugar a un valor erróneo en la salida. Esto conlleva que no se pueden conectar puertas PE en cascada.

En la figura 2 se muestra una puerta de la lógica PE que realiza la función X = (A + B) C, y que controla el inversor que genera X = Y. Suponiendo que durante la fase de precarga (Clk=’0’) se valida a la entrada el vector ABC=101, en la fase de evaluación, idealmente, las señales X e Y han de tomar los valores 0 y 1 respectivamente. Pero dado que en el instante en el que comienza la evaluación la señal X vale ‘1’, ésta se encuentra activando el transistor NMOS del inversor de salida, con lo que el nodo Y comienza a descargarse. No será hasta que la señal X pase por debajo del valor de activación del inversor (valor que en la fi gura se ha tomado como la mitad de la tensión de alimentación) que la señal Y deje de descargarse. Es decir, una señal que debería haber permanecido al valor de precarga VDD muestra un valor erróneo cuando se realiza una conexión en cascada. Esta lógica, de hecho, se presenta de forma meramente introductoria a las siguientes, que realizando modificaciones sobre la misma base mejoran éste y otros posibles inconvenientes.

 

Figura 2. Puerta X = (A+B)C en la lógica PE. Valor erróneo al realizar conexiones en cascada con la lógica PE (ABC=101)

Tecnología CMOS:

CMOS o MOSFET complementaria tiene una gran aplicación en el diseño de lógica de computadora. La relativamente alta impedancia de entrada, las rapidas velocidades de conmutación y los bajos niveles de potencia de operación de la configuración CMOS, han dado por resultado una disciplina totalmente nueva conocida como diseño de lógica CMOS.

Figura 3. CMOS inversor

Figura 4. Símbolos de los nMOS y pMOS

Marco conceptual:

Software Microwind:

Descripción: Microwind es una herramienta para diseñar y simular circuitos a nivel de diseño. Resulta engorroso, que siendo la primera vez que una persona trabaje en un software, se encuentre con una cantidad de términos desconocidos y no muy fáciles de entender. Microwind es uno de los paquetes donde más acontece esta dificultad, por tanto, es útil conocer algunos conceptos básicos del programa [2]:

- Tecnología de proceso: Consiste en un conjunto de reglas de diseño, que permiten construir circuitos integrados con determinadas características.

- Layout: Disposición de capas, o layers, que representan la litografía de dispositivos en un circuito integrado. En palabras más castizas, es un conjunto de máscaras, las cuales representan materiales, que son constitutivos de dispositivos a implementarse en un CI.

- Layer: Disposición de capas o mascaras que forman un Layout. Layers diferentes representan diferentes tipos de material, los cuales tienen usos específicos dentro de un layout.

- Lambda (𝝀): Es una escala de longitud que utiliza Microwind, para ajustar distancias a la tecnología empleada. No debe confundirse este lambda, con el lambda (𝜆) del modelo del modelo de segundo orden del transistor MOSFET operando en región de saturación. Para la tecnología, el valor lambda es ajustado a la mitad del largo del canal de un transistor MOS, por defecto.

Figura 5. Valor de lambda por defecto en Microwind

- Lambda grid: Es una cuadricula dispuesta sobre el workspace del microwind, escalada en lambdas, que sirve como referencia para ajustar distancias en la construcción de un layout.

Software DSCH:

Descripción:

El programa DSCH es un editor y simulador lógico. DSCH se utiliza para validar la arquitectura del circuito lógico antes de que se inicie el diseño microelectrónico. DSCH proporciona un entorno fácil de usar para el diseño de lógica jerárquica y una simulación rápida con análisis de retardo, que permite el diseño y validación de estructuras lógicas complejas.

DSCH también incluye los símbolos, modelos y soporte de montaje para los controladores 8051 y PIC16F84. Los diseñadores pueden crear circuitos lógicos para interactuar con estos controladores y verificar los programas de software usando DSCH.

Características:

- Entorno amigable para el usuario para el diseño rápido de circuitos lógicos.

- Admite el diseño de lógica jerárquica.

- Se agregó una herramienta sobre análisis de fallas a nivel de puerta de digital. Fallos: atascado en 1, atascado en 0. La técnica permite la inyección de una sola falla atascada en los nodos del circuito.

- Interfaz mejorada entre DSCH y Winspice.

- Maneja tanto la simulación lógica convencional basada en patrones como la simulación intuitiva en pantalla manejada por el mouse.

- Extractor incorporado que genera una lista de redes SPICE a partir del diagrama esquemático (Compatible con PSPICETM y WinSpiceTM).

- Genera una descripción VERILOG del esquema para la conversión del diseño.

- Acceso inmediato a las propiedades del símbolo (Delay, fanout).

- Soporte de modelo y montaje para microcontroladores 8051 y PIC 16F84.

- Soporte de tecnología submicrónica, submicrónica profunda y nanoescala.

- Apoyado por una enorme biblioteca de símbolos.

Figura 6. Multiplexor 74ls138 hecho con el software DSCH

DESARROLLO DEL TRABAJO:

    A)   De las siguientes preguntas del Laboratorio N° 4: 1, 2, 3, 5. Resolver como mínimo 02 (DOS) preguntas usando el programa DSCH y las indicaciones dadas.

Laboratorio Nº4: Pregunta 1

En primer lugar, analizamos la tabla de la verdad de la función booleana del ejercicio 1 que tiene 4 entradas:

Tabla 1. Tabla de la verdad

Ecuación booleana de la red pull-down:

El circuito expresado con transistores es el siguiente:

 

Figura 7. Circuito en el software DSCH obtenido a partir de la ecuación booleana

Pasamos ahora a crear el archivo “verilog” correspondiente al circuito:

Figura 8. Archivo verilog del ejercicio 1

Ahora exportamos el archivo verilog a microwind:

Figura 9. Layout del circuito del ejercicio 1

Comprobamos la ecuación encontrada con el comportamiento dinámico del layout, que debe ser igual que el análisis teórico:

 

Figura 10. Comportamiento dinámico del ejercicio 1

El comportamiento dinámico del circuito demuestra que las ecuaciones halladas teóricamente son correctas.

Área del layout

 

Figura 11. Medición del área del layout

Podemos darnos cuenta que el layout tiene un ancho de 317 𝜆 y de largo 226 𝜆, por lo que el layout tendrá un área total de: A_total=71642 λ^2=1119.406μm^2.

Frecuencia máxima de operación

La máxima frecuencia de operación está dado por la señal phi: f_maxima=1/T_phi =1/(1x10^(-9) )

f_maxima=1 GHz

Vista 3D

Figura 12. Transistores en el layout

Figura 13. Vista de corte 3D del Layout

Laboratorio Nº4: Pregunta 2

F(X1 , X2 , X3 , X4) = (X1 or X2 ) xor (X3 or X4 )

En primer lugar, analizamos la tabla de la verdad de la función booleana del ejercicio 2 que tiene 4 entradas:

Tabla 2. Tabla de la verdad

El circuito expresado con transistores es el siguiente:

Figura 14. Circuito en el software DSCH obtenido a partir de la ecuación booleana

Pasamos ahora a crear el archivo “verilog” correspondiente al circuito:

Figura 15. Archivo verilog del ejercicio 2

Ahora exportamos el archivo verilog a microwind:

Figura 16. Layout del circuito del ejercicio 2

Comprobamos la ecuación encontrada con el comportamiento dinámico del layout, que debe ser igual que el análisis teórico:

Figura 17. Comportamiento dinámico del ejercicio 2

El comportamiento dinámico del circuito demuestra que las ecuaciones halladas teóricamente son correctas.

Área del layout

 

Figura 18. Medición del área del layout

Podemos darnos cuenta que el layout tiene un ancho de 507 𝜆 y de largo 256 𝜆, por lo que el layout tendrá un área total de: A_total=129792 λ^2=2028μm^2.

Frecuencia máxima de operación

La máxima frecuencia de operación es la señal phi: f_maxima=1/T_phi =1/(0.8x10^(-9) )

f_maxima=1.25 GHz

Vista 3D

Figura 19. Transistores en el layout

 

Figura 20. Vista de corte 3D del layout

Laboratorio Nº4: Pregunta 3

G (X1 , X2 , X3 , X4) = F and X4                   F( X1 , X2 , X3 ) = X1 xor X2 xor X3

En primer lugar, analizamos la tabla de la verdad de la función booleana de F y G que tiene 4 entradas:

Tabla 3. Tabla de la verdad

En el caso de los CMOS domino se le pondrá un inversor a la salida, por lo que la ecuación booleana en el pull-down será:

En el caso de los CMOS domino se le pondrá un inversor a la salida, por lo que la ecuación booleana en el pull down será:

G=F and x_4

 

Figura 21. Circuito en el software DSCH obtenido a partir de la ecuación booleana

Pasamos ahora a crear el archivo “verilog” correspondiente al circuito: 

Figura 22. Archivo verilog del ejercicio 3

Ahora exportamos el archivo verilog a microwind:

 

Figura 23. Layout del circuito del ejercicio 3

Comprobamos la ecuación encontrada con el comportamiento dinámico del layout, que debe ser igual que el análisis teórico:

Figura 24. Comportamiento dinámico del ejercicio 3

El comportamiento dinámico del circuito demuestra que las ecuaciones halladas teóricamente son correctas.

Área del layout

Figura 25. Medición del área del layout

Podemos darnos cuenta que el layout tiene un ancho de 476 𝜆 y de largo 256 𝜆, por lo que el layout tendrá un área total de: 

A_total=121856 λ^2=1904μm^2.

Frecuencia máxima de operación

La máxima frecuencia de operación es la señal phi: f_maxima=1/T_phi =1/(0.8x10^(-9) )

f_maxima=1.25 GHz

Vista 3D

 

Figura 26. Transistores en el layout

Figura 27. Vista de corte 3D del layout

Laboratorio Nº4: Pregunta 5

F=A ̅(B ̅+C ̅D ̅)

En primer lugar, analizamos la tabla de la verdad de la función booleana de F que tiene 4 entradas:

Tabla 4. Tabla de la verdad

Figura 28. Circuito en el software DSCH obtenido a partir de la ecuación booleana

Ejemplos:

ABCD=1000 -> F=0

 

Figura 29. Comportamiento del circuito cuando ABCD=1000

ABCD=0100 -> F=1

Figura 30. Comportamiento del circuito cuando ABCD=0100

ABCD=1011->F=0

Figura 31. Comportamiento del circuito cuando ABCD=1011

ABCD=0000->F=1

Figura 32. Comportamiento del circuito cuando ABCD=0000

Pasamos ahora a crear el archivo “verilog” correspondiente al circuito:

Figura 33. Archivo verilog del ejercicio 5

Ahora exportamos el archivo verilog a microwind:

Figura 34. Layout del circuito del ejercicio 5

Comprobamos la ecuación encontrada con el comportamiento dinámico del layout, que debe ser igual que el análisis teórico:

Figura 35. Comportamiento dinámico del ejercicio 5

El comportamiento dinámico del circuito demuestra que las ecuaciones halladas teóricamente son correctas.

Área del layout

Figura 36. Medición del área del layout

Podemos darnos cuenta que el layout tiene un ancho de 255 𝜆 y de largo 155 𝜆, por lo que el layout tendrá un área total de: 

A_total=39525 λ^2=617.578μm^2.

Frecuencia máxima de operación

De la figura, nos damos cuenta que: f_maxima=1/t_(retraso maximo) =1/(820x10^(-12) )

f_maxima=1.22 GHz

Vista 3D

 Figura 37. Transistores en el Layout

 

Figura 38. Vista de corte 3D del Layout

 

    A)   Diseñe un circuito expandible (tipo matriz) MULTIPLICADOR para números en binario: A (n bits) / B (n bits). Diseño solo con circuitos combinacionales (sin reloj). 

1) Para números en binario natural para 4x4 bits.

Multiplicador en matriz

Este tipo de multiplicador paralelo se construye siguiendo el mismo procedimiento que la multiplicación manual. El multiplicando y el multiplicador forman una serie de productos parciales que deben sumarse hasta obtener el resultado final, el producto. La multiplicación está formada por la suma de tantas filas como bits tenga el multiplicando (m), donde cada fila tendrá tantos productos parciales como bits tenga el multiplicador (n). El retardo, en el peor caso, será el de la suma de m bits más la suma final de los dos últimos productos parciales de n bits. El retardo puede optimizarse sustituyendo la estructura RCA de la última fila del multiplicador por un sumador más rápido. El número total de celdas en función del número de bits del multiplicando y el multiplicador es de m×(n+1), es decir, n sumas parciales de m bits más el sumador final para completar el producto.

Figura 39. Arreglo de compuertas and para un multiplicador en matriz

 

Figura 40. Codificación de productos parciales

Creación de un sumador completo de 1 bit:

Figura 41. Defino la estructura del sumador

Figura 42. Doy click en “Schema to symbol” y defino mis entradas y salidas

Figura 43. Estructura lógica del esquemático

Realización de un multiplicador en matriz usando el software DSCH

Figura 44. Multiplicador para números binarios natural 4x4

Ejemplos:

(A=0100=4) x(B=0111=7) --> (F=00011100=28)

Figura 45. Funcionamiento de circuito cuando A=0100 y B=0111

(A=0010=2) x (B=0111=7) --> (F=00110110=14)

Figura 46. Funcionamiento de circuito cuando A=0010 y B=0111

(A=0110=6) x (B=1001=9) --> (F=00110110=54)

Figura 47. Funcionamiento de circuito cuando A=0110 y B=1001

(A=1111=15) x (B=1111=15) --> (F=11100001=225)

Figura 48. Funcionamiento de circuito cuando A=B=1111

Pasamos ahora a crear el archivo “verilog” correspondiente al circuito:

Figura 49. Archivo verilog del multiplicador de 4 bits

Ahora exportamos el archivo verilog a microwind:

Figura 50. Layout del multiplicador de 4 bits

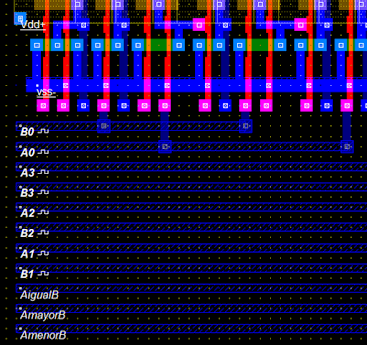
Figura 51. Entradas y salidas del multiplicador de 4 bits

 

Figura 52. Comportamiento dinámico del multiplicador de 4 bits

Área del layout

Figura 53. Medición del área del layout

Podemos darnos cuenta que el layout tiene un ancho de 970 𝜆 y de largo 290 𝜆, por lo que el layout tendrá un área total de: 

A_total=281300 λ^2=4395.3125μm^2.

Frecuencia máxima de operación

La frecuencia máxima será el inverso del retraso máximo. El retraso máximo es la diferencia entre el tiempo real en el que la salida debía cambio de valor y el tiempo ideal en el que debió ocurrir. 

De la figura, nos damos cuenta que: f_maxima=1/t_(retraso maximo) =1/(938x10^(-12) )

f_maxima=1.07 GHz

Vista 3D

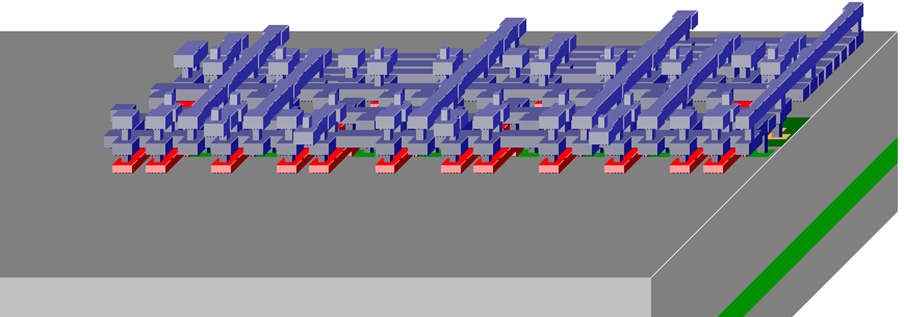
Figura 54. Transistores en el layout

Figura 55. Vista de corte 3D del Layout

2)Para números con signo en complemento a UNO para 4x4 bits. Asumir que las entradas y salidas ya deben estar en complemento de UNO. 

Complemento a 1 con 4 bits:

Tabla 5. Complemento a 1

Para el caso de los números en complemento a 1 de 4x4 bits. El numero cambia si el 4to bit es 1, los demás bits cambian por su complemento con respecto a su configuración en binario natural. Si permanece con “0” el 4to bit el número es el mismo en binario natural y en complemento a 1.

Figura 56. Multiplicador para números complemento a 1 4x4

Ejemplos:

(A=0100=4) x(B=0111=7) -->(F=0011100=28)

Figura 57. Funcionamiento de circuito cuando A=0100=4 y B=0111=7

(A=0110=6) x (B=1001=-6) -->(F=1011011=-36)

Figura 58. Funcionamiento de circuito cuando A=0110=6 y B=1001=-6

(A=1011=-4) x (B=1010=-5) -->(F=0010100=20)

Figura 59. Funcionamiento de circuito cuando A=1011=-4 y B=1010=-5

Pasamos ahora a crear el archivo “verilog” correspondiente al circuito:

Figura 60. Archivo verilog del multiplicador de complemento a 1 de 4 bits

Ahora exportamos el archivo verilog a microwind:

Figura 61. Layout del multiplicador de complemento a 1 de 4 bits

Figura 62. Entradas y salidas del multiplicador de complemento a 1 de 4 bits

Figura 63. Comportamiento dinámico del multiplicador de complemento a 1 de 4 bits

Área del layout

Figura 64. Medición del área del layout

Podemos darnos cuenta que el layout tiene un ancho de 4470  𝜆 y de largo 460 𝜆, por lo que el layout tendrá un área total de: A_total=2056200 λ^2=32128.125μm^2.

Frecuencia máxima de operación

La frecuencia máxima será el inverso del retraso máximo. El retraso máximo es la diferencia entre el tiempo real en el que la salida debía cambio de valor y el tiempo ideal en el que debió ocurrir. 

Nos damos cuenta que: f_maxima=1/t_(retraso maximo) =1/(5458x10^(-12) )

f_maxima=183.22 MHz

Vista 3D

Figura 65. Transistores en el layout

Figura 66. Vista de corte 3D del Layout

    A)   Diseñe un circuito expandible (tipo matriz) COMPARADOR para números en binario: A (n bits) / B (n bits). Diseño solo con circuitos combinacionales (sin reloj).

 

1) Para números en binario natural para 4x4 bits. 

Comparador

Un circuito digital comparador realiza la comparación de dos números A y B de N bits tomadas como un número entero sin signo e indica si son iguales o si una es mayor que otra en tres salidas A = B, A > B y A < B. Solo una de estas salidas estará a 1 y las demás estarán a 0 dependiendo de los valores de las entradas.

Comparador de 4 bits

En un comparador de 4 bits el procedimiento es el siguiente: 

- A=B Deben ser iguales cada uno de sus bits. 

-A>B Recorremos todos los bits de A y B desde el más significativo hasta que A sea 1 y B sea 0. 

- A< B. Recorremos todos los bits de A y B desde el más significativo hasta que A sea 0 y B sea 1.

Operación A=B:

Figura 67. Circuito lógico A=B

Función lógica booleana:

Operación A>B:

Función lógica booleana: 

Operación B>A:

Función lógica booleana:

Realización del comparador de 4 bits hecho en el software DSCH

Figura 68. Comparador para números binarios natural 4x4

Ejemplos:

(A=0100=4) > (B=0011=3)

Figura 69. Funcionamiento de circuito cuando A>B

(A=0110=6) < (B=1001=9)

Figura 70. Funcionamiento de circuito cuando B>A

(A=1111=15) = (B=1111=15)

Figura 71. Funcionamiento de circuito cuando A=B

Pasamos ahora a crear el archivo “verilog” correspondiente al circuito:

Figura 72. Archivo verilog del comparador de 4 bits

Ahora exportamos el archivo verilog a microwind:

Figura 73. Layout del comparador de 4 bits

 

Figura 74. Entradas y salidas del comparador de 4 bits

 

Figura 75. Comportamiento dinámico del comparador de 4 bits

Área del layout

Figura 76. Medición del área del layout

Podemos darnos cuenta que el layout tiene un ancho de 1175 𝜆 y de largo 270 𝜆, por lo que el layout tendrá un área total de: A_total=317250 λ^2=4957.03μm^2.

Frecuencia máxima de operación

La frecuencia máxima será el inverso del retraso máximo. El retraso máximo es la diferencia entre el tiempo real en el que la salida debía cambio de valor y el tiempo ideal en el que debió ocurrir. 

Nos damos cuenta que: f_maxima=1/t_(retraso maximo) =1/(4981x10^(-12) )

f_maxima=200.76 MHz

Vista 3D

Figura 77. Transistores en el layout

Figura 78. Vista de corte 3D del Layout

2) Para números con signo en complemento a DOS para 4x4 bits. Asumir que las entradas y salidas ya deben estar en complemento a DOS.

 Complemento a 2 con 4 bits:

Tabla 6. Complemento a 2

Para el caso de los números en complemento a 2 de 4x4 bits. La realización de la comparación en el 4to bit (bit de signo) cambia: El “1” lógico en el 4to bit representa un signo negativo y el “0” lógico representa un signo positivo. 

Para realizar un comparador con complemento a 2 partiendo del comparador binario natural, debemos comparar las salidas que tendremos en el 4to bit para ambas combinaciones:

Tabla 7. Diferencia en el 4to bit en un comparador complemento a 2 y binario natural

En caso de que el cuarto bit coincida en “0” o “1” para las entradas A y B, el análisis para los siguientes bits es el mismo que para el comparador binario natural.

Ejemplo:

A=0100=4 y B=0110=6 -> B>A. Si hacemos la comparación en binario natural en el primer, segundo y tercer bit se cumple que:110>100

A=1110=-2 y B=1101=-3 -> A>B. Si hacemos la comparación en binario natural en el primer, segundo y tercer bit se cumple que: 110>101 

Por lo tanto, solo debemos invertir la posición del cuarto bit: A4 por el B4 y viceversa. De esa manera creamos el comparador de bit en complemento a 2:

Figura 79. Comparador para números complemento a 2 4x4

Ejemplos:

(A=1100=-4)>(B=1010=-6)

Figura 80. Funcionamiento de circuito cuando A>B

(A=0100=4) < (B=0111=7)

Figura 81. Funcionamiento de circuito cuando A>B

(A=0110=6) > (B=1001=-7)

Figura 82. Funcionamiento de circuito cuando B>A

(A=1111=-1) = (B=1111=-1)

Figura 83. Funcionamiento de circuito cuando A=B

Pasamos ahora a crear el archivo “verilog” correspondiente al circuito:

 

Figura 84. Archivo verilog del comparador de complemento a 2 de 4 bits

Ahora exportamos el archivo verilog a microwind:

 

Figura 85. Layout del comparador de 4 bits

 

Figura 86. Entradas y salidas del comparador de complemento a 2 de 4 bits

 

Figura 87. Comportamiento dinámico del comparador de complemento a 2 de 4 bits

Área del layout

Figura 88. Medición del área del layout

Podemos darnos cuenta que el layout tiene un ancho de 1460 𝜆 y de largo 340 𝜆, por lo que el layout tendrá un área total de: A_total=496400 λ^2=7756.25μm^2.

Frecuencia máxima de operación

La frecuencia máxima será el inverso del retraso máximo. El retraso máximo es la diferencia entre el tiempo real en el que la salida debía cambio de valor y el tiempo ideal en el que debió ocurrir. 

Nos damos cuenta que: f_maxima=1/t_(retraso maximo) =1/(855x10^(-12) )

f_maxima=1.17 GHz

Vista 3D

Figura 89. Transistores en el layout

Figura 90. Vista de corte 3D del Layout

 

CONCLUSIONES:

   Ø  Con el software DSCH podemos crear los circuitos en lógica dinámica y estática. Aunque solo se puede simular en DSCH los circuitos en lógica estática.

   Ø  Para poder simular los circuitos en lógica dinámica o estática que creamos en el software DSCH, los podemos trasladar al software Microwind a través de un archivo verilog.

   Ø  Los multiplicadores en matriz son una manera muy útil de crear multiplicadores. Ya que se pueden ampliar si es que se necesita para una mayor cantidad de bits.

   Ø  El comparador es un conjunto de 4 circuitos (cuando A=B, cuando A>B y cuando B>A)

   Ø  La frecuencia de operación en los layouts extraídos de DSCH, por lo general son bajas comparados con los layouts de dimensión mínima creados por nosotros.

   Ø  El área de los layouts extraídos de DSCH es mayor que el área de los layouts de dimensiones mínimas creadas por nosotros.