Autor: Mauro Montoya Arenas
PROCESAMIENTO DIGITAL DE SEÑALES
🔴 En este articulo encontrarás:
Introducción
¿Qué son las señales?
Las señales son una representación de la evolución de un fenómeno en forma temporal y espacial, ya sea físico o de otra naturaleza. Las señales mas habituales son: La temperatura, la presión, el desplazamiento, el sonido o la voz, etc.
Se puede decir que las señales son funciones de variables independientes que contienen información. Matemáticamente, una señal x se puede representar como una función f que depende de las variables independientes x1, x2, x3, etc.
Tipos de señales
Los tipos de señales que existen son: analógicos, discretos, cuantizados y digitales. Cuando el tiempo es continuo y la amplitud es continua estamos hablando de una señal analógica. Cuando el tiempo es discreto y la amplitud es continua estamos hablando de una señal discreta. Cuando el tiempo es continuo y la amplitud es discreta estamos hablando de una señal cuantizada. Y cuando el tiempo es discreto y la amplitud es discreta estamos hablando de una señal digital.
Procesamiento digital de señales
Cuando hablamos de digitalizar una señal, nos referimos a que vamos convertir una señal analógica a una señal digital. Esto se realiza a través de un proceso que les explicare a continuación:
Primero obtenemos una señal analógica a través de un acondicionador de señal, después lo pasamos por un filtro pasa bajo para eliminar el ruido, seguidamente discretizamos la señal multiplicando la señal original por un tren de pulsos, a esta etapa es la que se conoce como muestreo de una señal.
El tren de pulsos tiene algunas características que influirán en la señal muestreada. Primero que todo, para que la señal no sufra un cambio de amplitud, el tren de pulsos tiene que tener una amplitud de 1. Además, la frecuencia de la señal discreta será la misma que la frecuencia del tren de pulsos.
Después haber discretizado la señal, la cuantizamos. Siguiendo con el ejemplo: Teníamos la siguiente señal discreta, esta señal tiene una amplitud continua, ya que esta puede tomar cualquier valor. Para cuantizar esta señal, vamos a suponer que solo pueden existir ciertos valores de amplitud, esos valores son: 0.25, 0.5, 0.75, 1, 1.25, 1.5, 1.75 y 2. Ahora vamos a aproximar la amplitud de cada muestra al valor mas cercano de los 8 valores permitidos que ya hemos nombrado. De esa manera, ahora la primera muestra tendrá un valor de 1.25, las siguientes 3 muestras tendrán un valor de 1.5, la siguiente muestra tendrá el valor de 1.25, las otras 3 muestras tendrán el valor de 1. Y las ultimas tres muestras tendrán el valor de 1.5, 1.75 y 2 respectivamente. Lógicamente, si la amplitud es discretizada a ciertos valores, se generara un error producto de que la amplitud de la señal dejo de ser continua. Además, como dijimos, la señal cuantizada tiene un tiempo continuo, es por ello, que mantendremos constante la amplitud de cada muestra hasta que lleguemos a la siguiente muestra.
Lo siguiente que debemos hacer es digitalizar la señal. Para eso, la señal cuantizada la pasamos por un conversor analógico digital, para convertir cada escalón de dicha señal en una señal digital de ceros y unos. Para nuestro ejemplo, suponemos que cada nivel puede ser expresado de la siguiente manera: el primer nivel discreto será 000, el segundo 001, el tercero 010, el cuarto 011, el quinto 100, el sexto 101, el séptimo 110 y el octavo 111.
De esa manera obtenemos la señal expresada en su forma digital, oséa, en ceros y unos.
Estos ceros y unos son captados y almacenados por nuestro sistema en tiempo discreto. Dicho sistema puede ser una computadora. Y así es como convertimos una señal analógica a digital, también podemos hacer el proceso inverso.
Desde nuestro sistema discreto podemos enviar una señal digital. A través de un conversor digital analógico podemos cuantizar dicha señal. Después utilizamos un filtro de reconstrucción para asemejar esa señal a una señal continua. Si es necesario podemos utilizar un amplificador para aumentar la amplitud de dicha señal. Después de haber pasado este proceso y si por ejemplo, la señal que trabajamos era una señal de voz, podemos usar un parlante como salida.
Señales en tiempo discreto
Las señales en tiempo discreto se obtienen mediante el muestreo de un señal continua en el tiempo y se representan como secuencias.
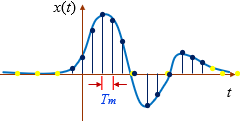
Esto se puede entender mejor con la siguiente grafica. Supongamos que tengo una función continua x(t). Si yo quiero pasar esta función a una señal discreta, primero tengo que muestrear dicha señal, con un periodo de muestreo igual a Tm. De tal forma que estoy obteniendo el valor de la señal continua solo en algunos puntos, y son con esos valores que formamos una señal discreta.
Matemáticamente las señales discretas se expresan de la siguiente manera:
Siendo x la señal discreta, n un numero entero que indica el tiempo discreto en el que existe la señal discreta y esto es igual a la variable continua de donde se extrae dicha señal discreta con un intervalo de muestreo Tm.
Para comprender esto mas a profundidad, veamos ahora el siguiente ejemplo:
Supongamos que tenemos la siguiente señal senoidal continua
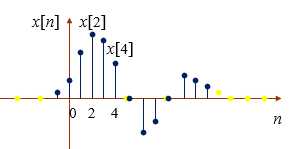
Si a esa señal continua nosotros pretendemos convertirla en una señal discreta, nos quedaría de la siguiente manera:
Si somos muy observadores, nos daremos cuenta que esta señal senoidal discreta tiene 33 valores discretos. La cantidad de valores discretos que se pueden obtener de una señal continua depende del tiempo de muestreo Tm, mientras mas pequeño sea el valor del tiempo de muestreo, mas muestras se podrán obtener. Por el contrario, si el tiempo de muestreo crece, se obtendrán menos valores discretos y la señal discreta se parecerá menos a la señal continua de la que se obtuvo.
Bien, ahora vamos a hablar sobre las secuencias básicas que existen en las señales discretas.
Empezando por la función impulso. Esta función se expresa a través de un delta. Va a valer 0 en todo el tiempo discreto, excepto cuando n=0, en ese caso tendrá un valor de 1. Tal y como podemos ver en la siguiente imagen:
Esta función expresada en Matlab seria de la siguiente manera:
% ---------------------------------
% FUNCION DELTA EN TIEMPO DISCRETO
% ---------------------------------
n=-3:3;
delta_n=[zeros(1,3) 1 zeros(1,3)];
stem(n,delta_n,'linewidth',3);
axis([-3 3 0 1.2]);
grid on;
xlabel('n');
ylabel('delta[n]');
title('delta[n] versus n')
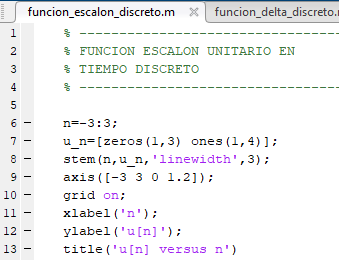
Otra función muy conocida es la función escalón. Esta función indica que la señal discreta "u[n]" va a ser 0 cuando el tiempo discreto n sea menor a 0. Y va a ser 1 cuando el tiempo discreto sea mayor o igual a 0. Como lo indica la siguiente imagen:
Esta función expresada en Matlab seria de la siguiente manera:
% ---------------------------------
% FUNCION ESCALON UNITARIO EN
% TIEMPO DISCRETO
% ---------------------------------
n=-3:3;
u_n=[zeros(1,3) ones(1,4)];
stem(n,u_n,'linewidth',3);
axis([-3 3 0 1.2]);
grid on;
xlabel('n');
ylabel('u[n]');
title('u[n] versus n')
Operaciones básicas
Desplazamiento en el tiempo
El desplazamiento en el tiempo ocurre cuando la señal discreta no empieza en el punto de referencia n=0. Es decir, que la señal no empieza en el tiempo 0. Esto se denota de la siguiente manera: Siendo "y[n]" la señal de salida igual a la señal "x" evaluado en n-k. Representando k el desplazamiento.
- Si k>0, se dice que corresponde a una operación de retardo. Oséa, la señal empieza después de n=0. En otras palabras, la señal esta retardada.
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
x[n] |
x[0] |
x[1] |
x[2] |
x[3] |
x[4] |
x[5] |
x[6] |
x[7] |
|
y[n]= x[n-1] |
x[-1] |
x[0] |
x[1] |
x[2] |
x[3] |
x[4] |
x[5] |
x[6] |
Si ahora suponemos que k=2. Obtendremos que y[n] es igual a dos tiempos pasados de x.
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
x[n] |
x[0] |
x[1] |
x[2] |
x[3] |
x[4] |
x[5] |
x[6] |
x[7] |
|
y[n]= x[n-2] |
x[-2] |
x[-1] |
x[0] |
x[1] |
x[2] |
x[3] |
x[4] |
x[5] |
- Si k<0, corresponde a una operación de adelanto. Oséa, la señal empieza antes de n=0. En otras palabras, la señal esta adelantada.
Esto se puede expresar con un diagrama de bloques. Si suponemos que k=-1, obtendremos lo siguiente: De entrada la señal discreta x, el bloque expresa un adelanto de 1, y esto nos da como señal discreta de salida y, que es igual a x evaluado en n+1.
Si hacemos una tabla comparativa podemos observar la diferencia entre x e y. Para un tiempo n dado, observamos que y[n] es igual a un tiempo futuro de x. Esto se da porque escogimos k=-1.
n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
x[n] | x[0] | x[1] | x[2] | x[3] | x[4] | x[5] | x[6] | x[7] |
y[n]= x[n+1] | x[1] | x[2] | x[3] | x[4] | x[5] | x[6] | x[7] | x[8] |
Si ahora suponemos que k=-2. Obtendremos que y[n] es igual a dos tiempos futuros de x.
n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
x[n] | x[0] | x[1] | x[2] | x[3] | x[4] | x[5] | x[6] | x[7] |
y[n]= x[n+2] | x[2] | x[3] | x[4] | x[5] | x[6] | x[7] | x[8] | x[9] |
Como ejemplo, vamos a realizar la siguiente programación en Matlab:
En este programa, generaremos un triangulo discreto de 21 muestras. Adicionalmente, le aplicaremos un desplazamiento en el tiempo de retardo y adelanto de 5 unidades. Primero declaramos el tiempo discreto en el va a existir el triangulo, que va a ser de 0 a 20, de 1 en 1. Después declaramos la variable del triangulo discreto, que va a ir de 0 a 10 de 1 en 1, y después va a descender de 1 en 1, de esa manera, generamos un triangulo discreto. Ahora vamos a colocar un subplot para separar la grafica en 3 partes, en la parte superior irá la señal triangulo discreto. Para plotear esta señal usamos el stem, con axis hacemos que el eje x vaya de -6 a 26 y el eje y que vaya desde 0 a 11. Ahora colocamos las grillas y sus respectivos títulos a cada eje y a la grafica.
Ahora, para realizar la operación de retardo, vamos a copiar todo desde el subplot. En el subplot vamos a cambiar este 1 por un 2 para graficarlo al medio. Como te había dicho, estamos realizando una operación de retardo de 5 unidades. Es por eso que en el stem vamos a sumarle 5 a la variable n. Con esto estamos haciendo que en el tiempo para la existencia de la señal triangulo discreto, empiece 5 posiciones después de n=0. Es decir, que estamos retardando la señal. Esto puede sonar un poco contrario, ya que para nuestro caso, la nomenclatura de x después de un retardo es de x evaluado en n-5. Pero cuando decimos que x esta evaluado en n-5 estamos diciendo que, si la señal antes empezaba en n=0, ahora va a empezar cuando n valga 5. Es por eso que en el stem estamos sumando 5 a nuestro tiempo discreto.
Finalmente, para realizar la operación de adelanto, volvemos a copiar todo desde el subplot. Y en el subplot vamos a cambiar este 1 por un 3 para graficarlo en la parte inferior. Como te había dicho, estamos realizando una operación de adelanto de 5 unidades. Es por eso que en el stem vamos a restarle 5 a la variable n. Con esto estamos haciendo que en el tiempo para la existencia de la señal triangulo discreto, empiece 5 posiciones antes de n=0. Es decir, que estamos adelantando la señal. Esto, al igual que la operación pasada puede sonar un poco contrario, ya que la nomenclatura de x después de un adelanto es de x evaluado en n+5. Pero cuando decimos que x esta evaluado en n+5 estamos diciendo que, si la señal antes empezaba en n=0, ahora va a empezar cuando n valga -5. Es por eso que en el stem estamos restando 5 a nuestro tiempo discreto.
Bien, con la programación lista, le vamos a dar a correr, y obtenemos las 3 graficas. En la parte superior, la señal triangulo discreto, en el medio la señal sometida a un retardo, y en la parte inferior la señal sometida a un adelanto.
% -------------------------------------------------------------
% Generación de señal discreta triangulo discreto de 21 muestras
% -----------------------------------------------------------------
% Intervalo de tiempo discreto
n=0:20;
%Valor de cada una de las 21 muestras
xn=[0:1:10 9:-1:0];
%Grafica de x[n]
subplot(3,1,1);
stem(n,xn,'b','linewidth',2);
axis([-6 26 0 11]);
grid on;
xlabel('n');
ylabel('x[n]');
title('x[n] vs n');
%Grafica de x[n-5]
subplot(3,1,2);
stem(n+5,xn,'b','linewidth',2);
axis([-6 26 0 11]);
grid on;
xlabel('n');
ylabel('x[n-5]');
title('x[n-5] vs n');
%Grafica de x[n+5]
subplot(3,1,3);
stem(n-5,xn,'b','linewidth',2);
axis([-6 26 0 11]);
grid on;
xlabel('n');
ylabel('x[n+5]');
title('x[n+5] vs n');
En algunas operaciones, se cambia la velocidad del muestreo de una señal mediante la adición o reducción de muestras.
- Si se adicionan mas muestras se llama Up-sampling (Interpolación). Las muestras que se adicionan son ceros insertados entre cada par de valores que sí pertenecen a la señal original. Matemáticamente se puede expresar de la siguiente manera: la señal discreta x, después de someterse a un up- sampling, va a ser evaluada para n/M. Siendo n, valores que van a ser múltiplos de M, para condicionar que n/M sea un valor entero. Cabe resaltar que M debe ser mayor a 1 y entero, para que se cumpla un up-sampling.
El up-sampling expresado en diagrama de bloques seria de la siguiente manera: La señal entrada es x[n] que va a someterse a un up-sampling, y nos da como resultado la señal interpolada xu[n]
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
x[n] |
x[0] |
x[1] |
x[2] |
x[3] |
x[4] |
x[5] |
x[6] |
x[7] |
|
y[n]= x[n/2] |
x[0] |
0 |
x[1] |
0 |
x[2] |
0 |
x[3] |
0 |
- Si en lugar de adicionar muestras, se quitan muestras, se llama Down-sampling (declinación). Matemáticamente se puede expresar de la siguiente manera: siendo la señal de salida "x_d" igual a "x" evaluado en la multiplicación de M (el factor de up-sampling) por n (el tiempo discreto). Si sometemos una señal a esta operación, solo se mostrará en la salida cada M-esima muestra, y las demás muestras serán quitadas. Cabe resaltar que M debe ser mayor a 1 y entero para que se cumpla un down-sampling.
El down-sampling expresado en diagrama de bloques seria de la siguiente manera: La señal entrada es x[n] que va a someterse a un down-sampling, y nos da como resultado la señal x_d[n]
Para entender mejor este concepto, vamos a realizar el siguiente ejemplo: Supongamos que M=2. Para este caso, cuando n=0, la señal de salida "y" va a ser x evaluado en 2*0, lo que significa que y[n] va a estar evaluado en x[0]. Si ahora n vale 1, y[n] debería ser evaluado en x[2]. Si n vale 2, y[n] va a ser evaluado en x[4]. Si n vale 3, y[n] va a ser evaluado en x[6]. Si suponemos que x[7] es la ultima muestra de la señal, y[n] solo existirá hasta y[3]. Podemos darnos cuenta que la salida solo toma muestras múltiplos del valor de M , que en este caso es 2, las demás muestras son descartadas. Si M valdría 3, solo se mostraría en la salida las muestras múltiplos de 3. Si M valdría 4, solo se mostraría en la salida las muestras múltiplos de 4 y así sucesivamente. Además, "y" tiene la mitad de duración de la señal de entrada "x". Esto también se debe al valor de M=2. Si M valdría 3, "y" duraría una tercera parte de "x". Si M valdría 4, "y" duraría una cuarta parte de "x", y así sucesivamente.
n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
x[n] | x[0] | x[1] | x[2] | x[3] | x[4] | x[5] | x[6] | x[7] |
y[n]= x[2n] | x[0] | x[2] | x[4] | x[6] | 0 | 0 | 0 | 0 |
Por ultimo, vamos a realizar el siguiente ejemplo en Matlab: Aplicaremos una adición y reducción de muestras a una señal triangular con un factor de 2.
Empezaremos declarando el tiempo discreto de dicha señal, que va a ir de -10 a 10. Después creamos el triangulo discreto, desde n=-10 hasta n=0, la señal va a ir de 1 en 1 de 0 a 10 y después va a descender hasta llegar a 0 desde n=0 hasta n=10. Ahora colocamos un subplot para plotear la grafica en la parte superior, el grosor de las líneas será de 2. El eje x irá de -20 a 20, y el eje y irá de 0 a 11. Colocamos las grillas, el titulo del eje x, el titulo del eje y y el titulo principal.
Ahora vamos a someter la señal a un up-sampling o interpolación. Esta señal irá de -20 a 20. Para crear la señal interpolada primero creamos una variable "y" de 41 ceros. Debe ser de longitud 41 porque la señal original tiene 20 muestras mas una muestra en n=0. La señal interpolada va a duplicar la duración de la señal original, por eso, para crear el vector "yn1", la longitud será de 20x2 mas la señal en n=0, que no sufre la interpolación.
Ahora, introduciremos los valores de la señal "x" entre cada 2 valores de "yn1". De esa manera generamos la interpolación.
Analicemos un momento esta operación:
En la línea anterior habíamos creado el vector "yn1" que contenía 41 ceros. Ahora, con esta operación yn1(1) va a ser igual al primer valor de x que sería 0, yn1(2) permanece con su valor de 0, yn1(3) va tomar el valor de x(2) que sería 1, yn1(4) permanece con su valor de 0, yn1(5) va tomar el valor de x(3) que sería 2, y así sucesivamente. De esta manera sometemos a "xn" a una interpolación.
Plotearemos la señal interpolada al medio, colocamos el stem para plotear dicha señal con un grosor de línea de 2, colocamos el axis, la grilla, los respectivos títulos de los ejes y el titulo principal.
Ahora graficaremos el down-sampling o declinación. Recordemos que con esta operación reducimos la cantidad de muestras. El tiempo discreto irá de -5 a 5. Ahora creamos el vector "yn2", que va a ser igual a cada valor de "x" con un intervalo de 2 muestras. Analicemos esta operación: estamos haciendo que yn2(1) valga lo que vale x(1), yn2(2) va a ser igual a x(3), x(2) no se mostrará en la salida, yn2(3) va a ser igual a x(5), x(4) no se mostrará en la salida, esta secuencia se repetirá en toda la señal. De esa manera generamos el down-sampling.
Ahora colocamos un subplot para graficar la señal en la parte inferior, después el stem para plotear la señal con un grosor de linea de 2. Y finalmente colocamos el axis, la grilla, los respectivos títulos de los ejes y el titulo principal.
% -------------------------------------------------------------
% Adiccion y reduccion de muestras de una señal triangulo discreto
% ---------------------------------------------------------------
% Triangulo discreto
n=-10:10; % Intervalo de extensión de x[n]
%Valor de cada una de las 21 muestras
xn=[0:1:10 9:-1:0];
%Grafica de x[n]
subplot(3,1,1);
stem(n,xn,'linewidth',2);
axis([-20 20 0 11]);
grid on;
xlabel('n');
ylabel('x[n]');
title('x[n] vs n');
% Up sampling
n2=-20:20; % Intervalo de extensión de x[n/2]
% Valor de las muestras
yn1=zeros(1,41);
yn1(1:2:41)=xn;
% Gráfica de x[n/2]
subplot(3,1,2);
stem(n2,yn1,'linewidth',2);
axis([-20 20 0 11]);
grid on;
xlabel('n');
ylabel('y[n]=x[n/2]');
title('x[n/2] vs n');
% Down sampling
n3=-5:5; % Intervalo de contraccion de x[2n]
% Valor de las muestras
yn2=xn(1:2:21);
% Gráfica de x[2n]
subplot(3,1,3);
stem(n3,yn2,'linewidth',2);
axis([-20 20 0 11]);
grid on;
xlabel('n');
ylabel('y[n]=x[2n]')
title('x[2n] vs n');
Visita nuestro canal de YouTube para mas contenido: https://www.youtube.com/channel/UC93Nt6sA-7r_S7EtGO44GeA
