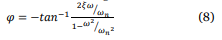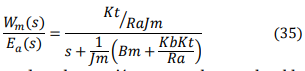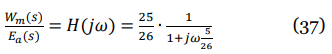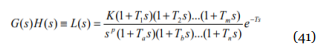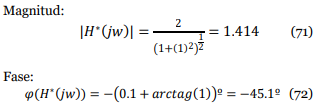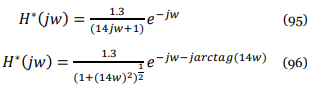Autores: Mauro Montoya Arenas
Leonel Breña Dávila
ANALISIS FRECUENCIAL
Resumen: En el presente documento hicimos énfasis en el análisis de un sistema de 2° orden específicamente del motor DC y la variación del parámetro inductivo de su armadura conlleva a tener otro tipo de respuesta que será evaluadas mediante un resultado de transferencia sin aproximar y uno simplificado a un sistema de 1° orden , además se detalla el proceso de obtención de respuesta temporal analíticamente usando la transformada inversa de Laplace para cada caso y para cada respuesta escalón , impulso y rampa unitaria en primera parte, luego se hace una deducción del resultado aproximado que, en efecto es válido para nuestro sistema con valor de inductancia cambiado y que tiene cierta condición justificándose matemáticamente. Finalmente se hizo un análisis de la obtención del resultado aproximado mostrado en Simulink y sus diferencias con el resultado real llegando a una conclusión que es concordante con lo analizado en el gráfico de polos y ceros.
I. INTRODUCCION
Hoy en día, el ingeniero cuenta con una amplia gama de herramientas computacionales que reducen los cálculos de forma exponencial, pero es importante saber que el análisis y la habilidad de interpretar resultados como gráficas que detallan el comportamiento de un sistema, o para este caso, su estabilidad, es una necesidad que siempre va a existir para los profesionales que llevan sus conocimientos a un nivel mayor que el simple empirismo. Bajo este contexto, se realizó el presente informe con el objetivo de detallar el proceso de obtención de gráficas de forma computacional y para contrastarlas con las obtenidas de forma manual, demostrando de esa forma, la suficiencia de tener una base teórica bastante solida siendo capaces que identificar cada detalle de la gráfica a realizar y una vez hecha, seremos capaces de interpretar la estabilidad relativa, datos que se encuentran implícitos en las gráficas de Bode y Nyquist. Además de lo ya mencionado, buscar la correlación entre ambos gráficos mostrará que contamos con un conocimiento bastante sólido en lo que la respuesta en frecuencia se refiere.
II. MARCO TEORICO
Diagramas de Bode
Cuando hablamos de respuesta en frecuencia en sistemas de control, es imposible no referirnos también a los diagramas de Bode. De acuerdo con [2], Un diagrama de Bode está formado por dos gráficas: una es la gráfica del logaritmo de la magnitud de la función de transferencia sinusoidal, y la otra es la gráfica del ángulo de fase; ambas se dibujan contra la frecuencia en escala logarítmica. El análisis que usaremos será la aproximación asintótica y dentro de esta, es de vital importancia conocer los casos principales a analizar
Término constante: Para la ganancia K, la magnitud es de 20 log10K y la fase es de 0°; ambas son constantes con la frecuencia. Por lo tanto, los diagramas de magnitud y de fase de la ganancia se indican en la figura 14.9. Si K es negativa, la magnitud sigue siendo de 20 log10 |K|, pero la fase corresponde a -180°.
Polo/cero en el origen: Para el cero (jꞷ) en el origen, la magnitud es de 20 log10ꞷ lo que se traduce en 20 dB/década, en tanto que la fase es constante con la frecuencia. y la fase corresponde a 90°. Los diagramas de Bode para el polo (jꞷ) -1 son similares, salvo que la pendiente del diagrama de magnitud sea de -20 dB/década, mientras que la fase es -90°. En general, para (jꞷ) N, donde N es un entero, el diagrama de magnitud tendrá una pendiente de 20N dB/década, mientras que la fase es de 90N grados.
Polo/cero simple: Para un cero simple (1 + jꞷ/z1), la magnitud es de 20 log10 |1+jꞷ/z1| y la fase equivale a tan-1 ꞷ/z1.
Notar que para ꞷ→0
20𝑙𝑜𝑔1 = 0 (1)
Para ꞷ→∞
20𝑙𝑜𝑔(𝜔/𝑧1) (2)
Lo que muestra que se puede aproximar la magnitud como cero (una línea recta con pendiente cero) para valores pequeños de ꞷ y mediante una línea recta con pendiente de 20 dB/década para valores grandes de ꞷ.
La fase tan-1(ꞷ/z1) se puede expresar como
Polo cuadrático/cero: La magnitud del polo cuadrático
Buscando los valores de extremo a extremo tenemos:
Por lo tanto, el diagrama de amplitud está compuesto de dos líneas rectas asintóticas: una con pendiente cero para ꞷ < ꞷn, y la otra con pendiente -40 dB/década para ꞷ>ꞷn, con ꞷn como la frecuencia de esquina (quiebre). Con respecto a la fase, la definimos de la siguiente manera:
Calculando el valor de la fase a distintos valores de frecuencia:
Con esto concluimos que El diagrama de la fase es una recta con
una pendiente de -90° por década, se empieza en ꞷn/10 y
termina en 10ꞷn.
Recalcamos que la aproximación asintótica es de bastante
utilidad para saber a grandes rasgos el comportamiento del
sistema en el dominio de la frecuencia. En un polo/cero
cuadrático, su diagrama real depende del factor de
amortiguamiento además de solo la frecuencia de esquina ꞷn
como se muestra en la siguiente imagen d.
Figura 1. Diagramas de Bode
Diagramas de Nyquist
El diagrama de Nyquist es una representación paramétrica de
una función de transferencia, se utiliza en control
automático y procesamiento de señales. El uso más común de
los diagramas de Nyquist es para la evaluación de la estabilidad
de un sistema con realimentación. La representación se realiza
en los ejes cardinales, esto es, la parte real de la función de
transferencia se representa en el eje X y la parte imaginaria se
traza en el eje Y. La frecuencia se recorre como un parámetro,
por lo que a cada frecuencia le corresponde un punto de la
gráfica. Alternativamente, en coordenadas polares, la ganancia
de la función de transferencia se representa en la coordenada
radial, mientras que la fase de la función de transferencia se
representa en la coordenada angular. El diagrama de Nyquist se
debe a Harry Nyquist, un exingeniero de los Laboratorios Bell
[3].
El diagrama de Nyquist, también es conocido como “La Traza
Polar” de una función de transferencia senoidal G(jω), es una
gráfica de la magnitud de G(jω) contra el ángulo de fase
de G(jω) en coordenadas polares, conforme ω varía de cero a
infinito. Por tanto, El diagrama de Nyquist es el lugar
geométrico de los vectores:
Figura 2. Ejemplo del diagrama de Nyquist
Figura 3. Mapeo de la function F(s)
Consideremos el sistema de control a lazo cerrado de la Figura 4:
Figura 4. Sistema realimentado
Entonces, en el Diagrama de Nyquist, el contorno que encierra
el semiplano derecho, que se muestra en la Figura 5, puede
mapearse a través de la función G(s)H(s), derivada de la Figura
4, sustituyendo puntos a lo largo del contorno en la función
G(s)H(s).
Figura 5. Semiplano derecho del Sistema de la figura 4
Estabilidad vía el Diagrama de Nyquist
Si un contorno, A, que rodea todo el semiplano derecho del
lugar de raíces del sistema determinado por la ecuación
característica 1+ G(s)H(s), se mapea a través de G(s)H(s),
entonces el número de polos del sistema a lazo cerrado, Z, en el
semiplano derecho, es igual al número de polos del sistema a
lazo abierto, P, que están en el semiplano derecho menos el
número de revoluciones en sentido antihorario, N, alrededor
de -1+j0 del plano complejo; es decir, Z:
II. MATERIALES Y METODOS
A. ESQUEMAS
B. PROCEDIMIENTO
01. Con la función de transferencia de segundo orden y los parámetros de la Tabla 1
a. Dibuja el siguiente diagrama en Simulink
Figura 10. Modelo de implementación
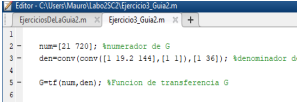
En el bloque Transfer Fcn, se debe escribir la función de transferencia de segundo orden del motor DC. La amplitud de la entrada siempre será 1 y la fase 0. Implementando en Simulink se obtuvo:
Figura 11. Implementación en Simulink
b. Grafica la respuesta del sistema para las siguientes frecuencias y completa la siguiente tabla.
Tabla 1. Valores de ganancia y fase para distintos valores de
frecuencia
Figura 12. Variación de la frecuencia de la entrada senoidal.
Obteniendo
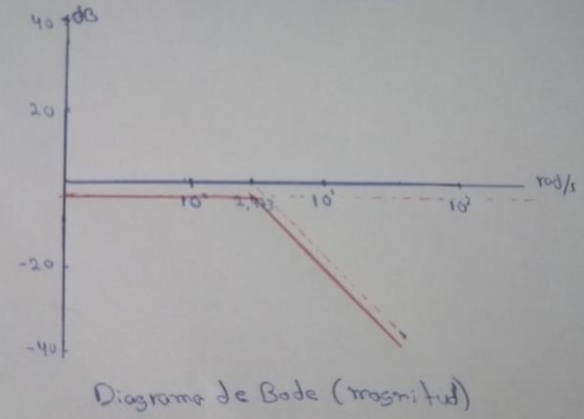
c. Realiza un esbozo de los diagramas de Bode. (Justifique y explique cada trazado de su esbozo).
La ecuación del sistema es la siguiente
La tabla con los valores de los parámetros se muestra a continuación:
Tabla 2. Parámetros de modelo de motor DC
Se realizó el diagrama de Bode considerando las asíntotas que
seguirá el sistema.
Iniciamos analizando la gráfica de magnitud, reemplazando en
la ecuación 14 con los valores de la tabla 2 se obtiene:
El diagrama de amplitud está compuesto de dos líneas rectas asintóticas, una con pendiente cero para ꞷ < ꞷn, y la otra con pendiente -40 dB/década para ꞷ > ꞷn, con ꞷn como la frecuencia de esquina (quiebre). Entonces, notamos que la frecuencia de esquina será ꞷn=2.473 y para el término constante K se obtiene
Figura 22. Diagrama de Bode para la magnitud
Para el diagrama de la fase es una recta con una pendiente de - -90° por década, se empieza en 𝜔n/10 y termina en 10𝜔n. Ya que podemos considerar tratar a este polo cuadrático como un polo doble si no consideramos el efecto que tiene el factor de amortiguamiento. La expresión para la fase sería:
Figura 23. Diagrama de Bode para la fase
Como el término constante es positivo, la fase de este se mantendrá en 0° y tenemos que la gráfica se realiza a -90° por década en una década anterior y posterior de la frecuencia de esquina ꞷn=2.473. d.
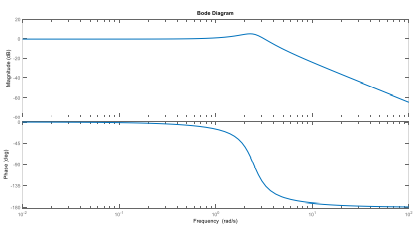
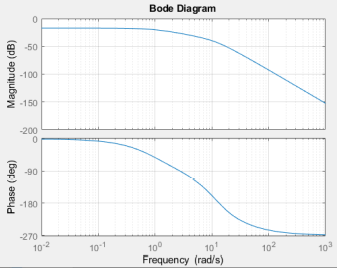
d. Realiza los diagramas de Bode con el comando de Matlab (Bode) y compara las curvas obtenidas con los resultados de fase y magnitud de la Tabla 2.
Primero se generó los diagramas de Bode del sistema
Figura 24. Gráficas de bode obtenida en Matlab
Luego, se realizó el acercamiento para cada frecuencia de interés de la tabla 1.
Figura 25. Acercamiento en 0.01 rad/s
e. Realiza un esbozo del diagrama de Nyquist. (Justifique y explique cada trazado de su esbozo).
Tener en cuenta los siguientes valores que fueron calculados en el análisis de Bode.
Evaluamos entonces:
- Para 𝜔 → ∞
- Para 𝜔 = 0
- Para 𝜔 = 𝜔𝑛
Figura 34. Diagrama de Nyquist
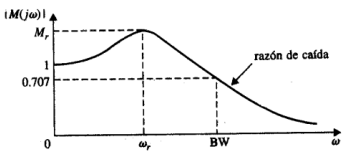
f. Realiza el diagrama de Nyquist con el comando de Matlab (Nyquist). Muestra y explica, de manera detallada, las correspondencias entre los diagramas de Bode y el diagrama de Nyquist.
Figura 35. Diagrama de Bode obtenida en Matlab
Figura 36. Diagrama de Nyquist obtenida en Matlab
Habiendo mostrado el diagrama de Bode y Nyquist, analizaremos distintos puntos para ver la correlación y lo que representan en cada gráfica. Cuando ꞷ→0 obtuvimos en g, nos da un valor de magnitud equivalente al término constante K=0.96, que viene a ser el punto de inicio del diagrama de Nyquist. Para la fase, es fácil apreciar que el ángulo es de 0°, pues se encuentra la recta real de la gráfica Para hallar la relación entre Nyquist y Bode, debemos recordar que los diagramas de Bode son elaborados en dB, entonces, deberemos hacer la transformación respectiva a los valores de magnitud hallados en Nyquist.
Identificando el punto inicial de Nyquist en el diagrama de
Bode:
Transformando el término constante a dBs (en ꞷ→0.01 como
aproximación, ya que trabajamos en escala logarítmica)
obtenemos que
Ubicando el punto inicial en los diagramas de Bode:
Figura 37. Ubicando el punto inicial de Nyquist en Bode
Haciendo un acercamiento obtenemos
Figura 38. Acercamiento de los diagramas de Bode
Identificando el punto final de Nyquist en el diagrama de Bode:
Según [2], para altas frecuencias tales que ꞷ>>ꞷn la magnitud
logarítmica para el diagrama de Bode es
Lo que nos indica que la asíntota de alta frecuencia (infinito por practicidad) es una recta con pendiente de -40 dB/década, quiere decir que si consideramos la gráfica de Bode a altísimas frecuencias, en nuestro sistema que tiene un polo cuadrático, en Nyquist se verá reflejado en el origen de coordenadas cuando en Bode significará una recta con pendiente de -40 dBs.
Identificando el punto de ꞷ=ꞷn de Nyquist en el diagrama de
Bode:
En la parte g, realizamos los cálculos para este valor de
frecuencia y se obtuvo que para ꞷ=ꞷn (con ꞷn=2.473) teníamos
una magnitud de 1.73 y una fase de -90, como se evidencia
también en la figura 36 (ya que el punto es perpendicular al
origen. Para ver su correlación con los diagramas de Bode
transformamos primero este valor de magnitud a dB
20𝑙𝑜𝑔1.73 = 4.76 𝑑𝐵 (33)
Ubicando el diagrama de Bode a esta posición tenemos
Figura 39. Ubicación para ꞷ=ꞷn en Bode
Haciendo un acercamiento obtenemos:
Figura 40. Acercamiento de los diagramas de Bode
g. Con todas estas simulaciones
i. Sabiendo que la entrada de la función de
transferencia es el voltaje de la armadura y la
salida es la velocidad del motor, ¿qué puedes
concluir después de hacer todas estas
simulaciones?
Podemos decir que, ante la entrada de voltaje del motor
en la armadura, la salida (velocidad) será de la misma
frecuencia, pero, dependiendo del valor de esta, se
determinarán los valores de amplitud como de
corrimiento en la fase. Podemos ver en la figura 24, que
a valores de frecuencia anteriores a una década
anterior a 𝜔𝑛 = 2.473 se iniciarán a mostrar cambios
significativos en el motor, como la amplificación de la
magnitud y el corrimiento de la fase.
ii. Compara y comenta las fases de los casos con
frecuencias de 0.5rad/s y 3.17rad/s.
Al ver las gráficas a estos 2 sistemas, podemos afirmar
que tienen magnitudes aproximadamente iguales, pero
a distintos valores de fase. La coincidencia en el valor
de magnitud se debe al efecto del factor de
amortiguamiento es
Dato que se obtuvo en el análisis de Nyquist. Además [1] nos dice: Nótese que el diagrama real depende del factor de amortiguamiento ξ, así como de la frecuencia de esquina (ruptura) ωn. En la figura 1, en el marco teórico, se muestra la respuesta del sistema ante diversos valores de factor de amortiguamiento, y al nosotros tener uno de 0.278, es decir <1, la presencia de un pico con un valor de resonancia en la cima era el esperado, eso quiere decir que habrá 2 puntos con el mismo valor de magnitud, antes y después del valor de resonancia.
iii. ¿Qué puedes afirmar acerca de la estabilidad
del sistema?
Vemos que el sistema es estable ante los valores de los
parámetros dados. La magnitud del sistema se verá
prácticamente totalmente atenuada por a medida que
la frecuencia se eleva, además de ellos, para evitar picos
muy elevados en la respuesta de magnitud, sería
necesario variar los parámetros de tal forma que el
factor de amortiguamiento se acerque más a la unidad.
La fase tendrá un desplazamiento máximo de 180°
conforme a las gráficas de Bode. Respecto a Nyquist,
podemos decir que la gráfica no encierra al punto -1, lo
que nos reafirma la estabilidad del sistema.
02. Cambia el valor de la inductancia a La= 0.1H . Con esto podemos lograr un modelo simplificado del motor de primer orden, que es el siguiente:
a. Define este modelo simplificado del motor de la ecuación 2
Reemplazando en la ecuación 35 por valores en la tabla
2 obtenemos
Dándole forma para obtener el modelo de polo simple:
De aquí se obtiene el valor del término constante y del
polo simple, entonces para el gráfico de magnitud y de
fase se obtienen de la siguiente forma:
Donde identificamos que la frecuencia de esquina es:
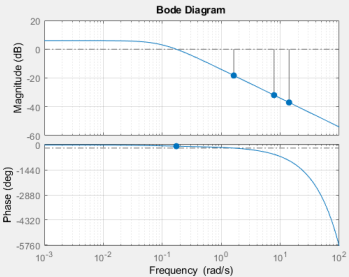
b. Compara la respuesta en frecuencia (diagrama de Bode y diagrama de Nyquist) de ambos modelos (ecuacion1 y ecuación 2). ¿Hasta qué frecuencia dirías que la aproximación de primer orden es válida? ¿Por qué?
Figura 41. Gráficas de bode para el modelo simplificado.
c. Compara los márgenes de estabilidad relativa para ambos modelos
d. Documente y describa la implementación y los resultados obtenidos.
Para analizar los márgenes de estabilidad tenemos que pensar
en el sistema como un sistema en lazo cerrado donde se
encuentra un K en serie con la función de transferencia.
Podemos decir que el sistema simplificado funcionará
correctamente para valores de baja frecuencia menores de 1rad/s ya que a partir de este valor el sistema completo
comenzará a sufrir efectos de su coeficiente de amortiguamiento
y llegará eventualmente a su valor de resonancia, ejemplo a ello,
mostraremos la respuesta a su valor de frecuencia natural 𝜔𝑛.
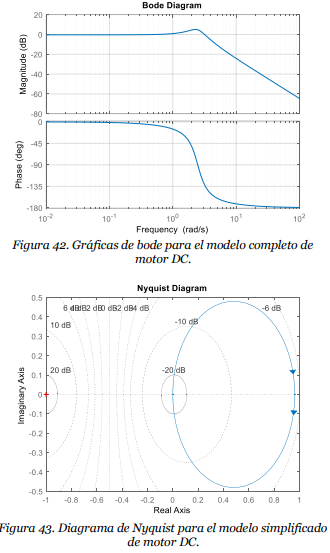
El resultado es el esperado, ya que en la figura 42 para el sistema completo vemos que, al valor de la frecuencia natural, el sistema presenta un aumento en su magnitud y un corrimiento de fase de -90°, mientras que para el modelo simplificado vemos que presenta una pequeña atenuación y un corrimiento de fase de 21° aproximadamente. De igual manera, mostraremos las respuestas frecuenciales a un valor de frecuencia menor a la unidad (ꞷ=0.5 rad/s)
3. Estabilidad relativa
a. Defina y explique claramente cuáles son los parámetros de estabilidad relativa.
Estabilidad relativa: La estabilidad relativa mide cuan estable es un sistema. en el dominio de la frecuencia, el pico de resonancia M se puede emplear para indicar la estabilidad relativa. Otra forma de medir la estabilidad relativa en el dominio de la frecuencia es observando q tan cerca se encuentra la traza de Nyquist de L(jw) del punto (-1,j0).
Pico de resonancia: Es un indicador de la estabilidad del sistema en lazo cerrado. De hecho, cuando el polo esté más cerca al eje imaginario, el pico crece cada vez más hasta llegar al infinito
Figura 53. Mr en el diagrama de bode
Si tengo:
Los casos evaluados para la estabilidad relativa son los siguientes:
1) Caso (a): ganancia de lazo K baja. La traza de Nyquist de L(jw) intersecta al eje real negativo en un punto muy lejano a la derecha del punto (-1,j0). La respuesta al escalón está bien amortiguada, y el valor de Mr, de la respuesta en frecuencia es bajo.
Figura 54. Sistema estable y bien amortiguado
2) Caso (b): K se incrementa. La intersección se mueve cerca del punto (-1,j0); el sistema es aún estable, ya que el punto crítico no está encerrado, pero la respuesta al escalón tiene un sobreimpulso máximo grande, y Mr también es grande.
Figura 55. Sistema estable y oscilatorio
3) Caso (c): K se incrementa más. La traza de Nyquist ahora pasa a través del punto (-1,j0), y el sistema es marginalmente estable. La respuesta al escalón se vuelve oscilatoria con amplitud constante, y Mr se vuelve infinita.
Figura 56. Sistema marginalmente estable
4) Caso (d): K es relativamente grande. La traza de Nyquist encierra al punto (- 1,j0), y el sistema es inestable. La respuesta al escalón se vuelve no acotada. La curva de magnitud del módulo de |M(jw)| en función de w deja de tener significado. De hecho, el sistema es inestable pero el valor de Mr es todavía finito.
Figura 57. Sistema inestable
b. Defina en Matlab la siguiente función de transferencia.
G(s)=(24s+720)/((s^2+19.2s+144)(s+1)(s+36)) (42)
Figura 58. Defino G(s) en Matlab
c. Obtén los parámetros de estabilidad y muéstralos en los diagramas de Bode. Adicionalmente, puedes utilizar la función margin para encontrar directamente los parámetros de estabilidad.
Para desarrollar este enunciado utilizamos primero la función Bode:
Figura 59. Aplico Bode al sistema G(s)
Si le doy a correr obtengo el diagrama de Bode:
Figura 60. Diagrama de bode hecho con la función “bode” de Matlab
Para ver los márgenes de estabilidad en el diagrama de bode primero damos clic derecho en la gráfica, seleccionamos “characteristic” y después “All Stability Margins”
Figura 61. Mostramos la estabilidad
Figura 62. Márgenes de la función G(s) de Bode
Como se puede ver en la figura 63. Solo existe margen de ganancia positiva (sistema estable). Ahora utilizamos la función “margin” para encontrar los márgenes de manera inmediata.
Con la función “margin” de hecho podemos observar también la frecuencia “w” en donde la fase en -180º y el valor de la magnitud en dB a esa frecuencia.
d. Dibuja los márgenes de fase y de ganancia sobre la gráfica polar. Compáralos con los obtenidos mediante el diagrama de bode. ¿Se corresponden?
Con la función de Nyquist podemos observar la gráfica polar del sistema. Para ver los márgenes aplicamos el mismo procedimiento que hicimos en la gráfica de bode: damos clic derecho en la gráfica, seleccionamos “characteristic” y después “All Stability Margins”.
Figura 65. Seleccionamos “All Stability margin” para ver los márgenes del sistema
Tambien seleccionamos “show” y desmarcamos “negative frecuencies”
Figura 66. Anulamos el diagrama para frecuencias negativas
Después de ejecutar los procedimientos señalados. La grafica nos quedara de la siguiente manera:
Figura 67. Diagrama de Nyquist que muestra las frecuencias positivas y los márgenes de estabilidad
Para visualizar los márgenes de estabilidad le vamos a dar zoom a la imagen:
Figura 68. Le hacemos un acercamiento a la gráfica para visualizar el margen de estabilidad
Por la gráfica de la figura 68. Podemos sacar las siguientes conclusiones:
Para comparar si este valor es correcto reemplazamos w=13.4 rad/s en H(w) y hallamos la parte real e imaginaria. En la figura 69 se muestra H(w=13.4):
Figura 69. H(w) cuando w=13.4 rad/s
De la imagen se desprende que:
Si comparamos la ecuación ___ con las ecuaciones ___, podemos ver que el diagrama de Nyquist marca el valor correcto de la parte real e imaginaria de H(w).
e. Determine el valor de ganancia K (K crítico) que hace inestable al sistema en lazo cerrado. Muestre la respuesta temporal de lazo cerrado del sistema para los siguientes valores:
Definimos “K” como la ganancia que acompaña en serie al sistema “G(s)”.
Hallamos Kcritico: Para hallar “Kcritico” recurrimos a la función margin y le colocamos como parámetros de entrada “Gm”, “Pm”, “Wcg” y “Wcp”. Gm nos dará el valor de K.
Figura 70. Obtenemos Kcritico a partir de la función “margin”
De la función obtuvimos que Kcritico=170.2645. Introducimos ahora “K” en serie a nuestra función y vemos que ocurre cuando en la entrada colocamos una señal escalón unitario:
Figura 71. Sistema G(s) en serie con K (al nuevo sistema lo nombramos Gk)
Probamos entonces el sistema Gk para K=160 (K<Kcritico), K=170.2645 (K=Kcritico) y K=200 (K>Kcritico)
i. K< Kcrítico.
Para K=160, analizamos las siguientes graficas:
Figura 72. En el diagrama de Bode vemos que para una fase(Gk)=-180º, |Gk|<0 dB (estable)
Figura 73. En el diagrama de Nyquist vemos que Gk(s) con K=160 no toca al punto (-1,j0) y pasa por la derecha (sistema estable)
Figura 74. Polos y ceros para Gk(s) cuando K=160
Figura 75. Gk(s) con K=160 y una entrada escalón unitario
Análisis: Podemos ver que los polos de Gk(s) están muy cerca al eje imaginario, eso significa que el sistema será muy oscilatorio, pero finalmente se pondrá estable, tal como lo muestra la figura ____.
ii. K=Kcrítico.
Para K=170.2635, analizamos las siguientes graficas:
Figura 76. En el diagrama de Bode vemos que para una fase(Gk)=-180º, |Gk|=0 dB (oscilatorio)
Figura 77. En el diagrama de Nyquist vemos que Gk(s) con K=170.2635 toca al punto (-1,j0) (sistema oscilatorio)
Figura 78. Polos y ceros para Gk(s) cuando K=170.2635
Figura 79. Gk(s) con K=170.2635 y una entrada escalón unitario
Análisis: Podemos ver que los polos de Gk(s) están en el eje imaginario, eso significa que el sistema será oscilatorio, tal como lo muestra la figura 79.
ii. K>Kcrítico.
Para K=200, analizamos las siguientes graficas:
Figura 80. En el diagrama de Bode vemos que para una fase(Gk)=-180º, |Gk|>0 dB (inestable)
Figura 81. En el diagrama de Nyquist vemos que Gk(s) con K=200 pasa al punto (-1,j0) por el lado izquierdo (sistema inestable)
Figura 82. Polos y ceros para Gk(s) cuando K=200
Figura 83. Gk(s) con K=200 y una entrada escalón unitario
Análisis: Podemos ver que los polos de Gk(s) están en la parte positiva del eje real, eso significa que el sistema será inestable, tal como lo muestra la figura.
f. Documente y describa la implementación y los resultados obtenidos.
Análisis de resultados: Podemos observar en este caso que el sistema solo presenta margen de ganancia. El Kcritico pudimos hallarlo utilizando la función “margin” (20log(Kcritico)=Distancia entre la magnitud y el 0 en dB). Hemos analizado el sistema en serie con K en 3 situaciones posibles: estable, oscilatorio e inestable, es decir, variamos el K e introducimos una señal de entrada escalón. El sistema se comportará de manera diferente conforme se varíe K. Par cada valor de K hemos obtenido su respectivo diagrama de bode y de Nyquist, para verificar la estabilidad o inestabilidad del sistema.
04. Efecto del retardo de tiempo
a. Esboza la respuesta en frecuencia (diagrama de Bode y Nyquist) de un retardo puro de 1 segundo. (Justifique y explique cada trazado de su esbozo).
Como función de transferencia del sistema probaremos la siguiente función de transferencia:
Análisis del diagrama de Bode y Nyquist
Para saber cómo se origina la gráfica de bode que se obtiene de G(s) desplazado un segundo. Tendremos que analizarlo de forma matemática convirtiendo s=jw:
Ecuación de la magnitud:
Ecuación de la fase:
Sea w->0:
Magnitud:
Fase:
Cuando w tiende a 0. La magnitud en decibelios de
H(jw) se encuentra en 6.02dB y su fase en 0º.
Análisis y explicación de la gráfica de Nyquist
Para saber cómo se origina la gráfica de Nyquist que
se obtiene de H(s) desplazado un segundo.
Tendremos que analizarlo de forma matemática
convirtiendo s=jw:
Ecuación de la magnitud:
Ecuación de la fase:
Sea w->0 (punto de inicio):
Sea w=0.1/τ=0.01:
Sea w=1/τ=0.1:
Sea w=10/τ=1:
Sea w->∞ (punto final):
Figura 84. Esbozo del diagrama de Bode (magnitud en
dB) de la ecuación 46
Figura 85. Esbozo del diagrama de Bode (fase en grados
sexagesimales) de la ecuación 46
Figura 86. Esbozo del diagrama de Nyquist de la
ecuación 46
b. Obtenga la respuesta en frecuencia (diagrama de Bode y Nyquist) utilizando los comandos de Matlab respectivos.
Figura 87. Script para hallar los diagramas de Bode y
Nyquist
Figura 88. Diagrama de Bode de la ecuación 46
Figura 89. Diagrama de Nyquist de la ecuación 46
Figura 90. Diagrama de bode de la ecuación 46
c. Hallar la respuesta en frecuencia de H(s)
Figura 91. Script para hallar los diagramas de Bode y Nyquist
Figura 92. Diagrama de Bode de H(s)
Figura 93. Diagrama de Nyquist de H(s)
Para comprobar que el sistema es estable y que empieza desde el tiempo t=0, hallamos la respuesta del sistema con una función de entrada escalón:
Figura 94. Respuesta del sistema H(s) con na entrada escalón
d. Analizar y explica con detalle el efecto que casusa la adición a H(s) de un retardo de 1s en su respuesta en frecuencia.
Figura 95. H(s) considerando el retardo
Análisis y explicación de la gráfica de Bode
Para saber cómo se origina la gráfica de bode que se obtiene de H(s) desplazado un segundo. Tendremos que analizarlo de forma matemática convirtiendo s=jw:
Ecuación de la magnitud:
Ecuación de la fase:
Sea w->0:
Cuando w tiende a 0. La magnitud en decibelios de H(jw) se encuentra en 2.279 dB y su fase en 0º.
Figura 96. Punto en magnitud y fase del diagrama de bode cuando w->0
Sea w=0.1/τ=7.143x10^(-3):
Cuando w es igual a 0.1/τ. La magnitud en decibelios de H(jw) sigue siendo 2.279 dB y su fase desciende ligeramente de 0º a -5. 8º.
Sea w=1/τ=7.143x10^(-2):
Cuando w es igual a 1/τ. La magnitud en decibelios de H(jw) se reduce a -0.7313 dB y su fase desciende a -45.7º.
Figura 97. Punto en magnitud y fase del diagrama de bode
cuando w=1/τ
Sea w=10/τ=7.143x10^(-1):
Cuando w es igual a 10/τ. La magnitud en decibelios de H(jw) es -17.721 dB y su fase desciende a -94.3º.
Sea w->∞:
Cuando w tiende a ∞. La magnitud en decibelios de H(jw) se estabilizará a un valor de -20log(w) dB y su fase desciende a –w.
Figura 98. Diagrama de Bode de H(s)
Análisis y explicación de la gráfica de Nyquist
Para saber cómo se origina la gráfica de Nyquist que se obtiene de H(s) desplazado un segundo. Tendremos que analizarlo de forma matemática convirtiendo s=jw:
Ecuación de la magnitud:
Ecuación de la fase:
Sea w->0 (punto de inicio):
Cuando w tiende a 0. La magnitud de H(jw) se encuentra en 1.3 y su fase en 0º.
Figura 99. Punto de inicio en el diagrama de Nyquist
Sea w=0.1/τ=7.143x10^(-3):
Cuando w es igual a 0.1/τ. La magnitud de H(jw) sigue siendo prácticamente 1.3 y su fase desciende ligeramente de 0º a -5. 8º.
Sea w=1/τ=7.143x10^(-2):
Cuando w es igual a 1/τ. La magnitud de H(jw) desciende ligeramente a 0.919 y su fase llega a -45º.
Figura 100. Diagrama de Nyquist apuntando el punto cuando w=1/τ
Sea w=10/τ=7.143x10^(-1):
Cuando w es igual a 10/τ. La magnitud de H(jw) pasa a ser 0.13 y su fase desciende hasta -94.3.
Sea w->∞ (punto final):
Figura 101. Punto final en el diagrama de Nyquist
Cuando w tiende a ∞. La magnitud de H(jw) tiene la forma de 1/w y su fase tiene la forma de –wº (esta es la razón por la que existen vueltas alrededor del punto final). Como wº siempre aumentara su valor, este va generando vueltas conforme w va aumentando.
Figura 102. Diagrama de Nyquist de H(s)
Para comprobar que el sistema es estable y que empieza y que tiene un retardo de t=1 segundo, hallamos la respuesta del sistema con una función de entrada escalón:
Figura 103. Respuesta del sistema H(s) con na entrada escalón
e. Documente y describa la implementación y los resultados obtenidos.
Análisis de resultados: Se comprobó el efecto que tiene el
retraso en la estabilidad de un sistema. ya que este retraso
(por más pequeño que sea), puede hacer que el sistema sea
inestable. Con los diagramas de Bode y Nyquist pudimos
hallar los márgenes de ganancia y fase del sistema con
retraso en lazo cerrado para calcular el Kcritico (siendo K
una constante). Este análisis adicional nos permite saber
cuál debe ser el valor máximo de una constante en serie con
el sistema.
III. CONCLUSIONES
Se comprobó la correlación entre las gráficas de Bode y Nyquist en el apartado 1 parte f, interpretando los puntos resaltado en Nyquist y encontrando su analogía en las gráficas de Bode.
Vimos los efectos del factor de amortiguamiento, factor que afecta en gran medida a la respuesta frecuencial, ya que la deforma en gran medida, creando picos y una respuesta que pasa muy por debajo de la frecuencia de esquina ꞷn y en el caso de Nyquist define el tamaño del lóbulo de la gráfica dependiendo de qué tipo de sistema sea, en el caso de el apartado 1, fue un sistema
subamortiguado.
Al comparar el modelo simplificado con el completo del motor DC de los apartados 1 y 2, concluimos que se pueden aproximar si escogemos valores de frecuencia menores ala unidad, pues a partir de ese valor, los efectos del factor de amortiguamiento comienzan a actuar. Además de que el modelo simplificado es de primer orden y por ello solo puede tener una fase máxima de 45°, a diferencia del real, que llega hasta 180°.
Los retrasos influyen en el comportamient0 de la función de transferencia con respecto a la frecuencia (esto lo podemos ver en los diagramas de Bode y Nyquist)
Cuando una función de transferencia esta en serie con K y en lazo cerrado, puede ocurrir 3 posibles estados: K<Kcritico (el sistema es estable), K=Kcritico (el sistema es oscilatorio) y K> Kcritico (el sistema es oscilatorio)
Si introducimos una señal escalon unitario podemos comprobar la estabilidad o inestabilidad del sistema. Ademas si K<Kcritico podremos saber si el sitema es citicamente, cobre o sub amortiguado.
IV. REFERENCIAS
[1]: Matthew N. O. Sasiku. Fundamentos de Circuitos Eléctricos. Cap. 14.
[2] Katsuhiko Ogata. Teoría de Control Moderna. Cap. 7.
[3]:https://es.wikipedia.org/wiki/Diagrama_de_Nyquist#:~:text=El%20diagrama%20de%20Nyquist%20es,de%20un%20sistema%20con%20realimentaci%C3%B3n.
[4]: https://dademuch.com/2020/02/15/el-diagrama-de-nyquist
