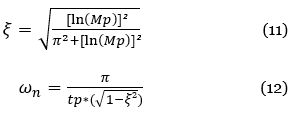Terry Quispe Paniagua (terryfiee2021@gmail.com)
Informe final N°6: Identificación de Sistemas
A medida que vamos estudiando y viendo más sobre los sistemas de primer y segundo orden, vemos la necesidad de aplicar métodos que nos faciliten la representación de los mismos , es decir si tenemos un sistema el cual se desconoce su física interna o es demasiado complicado saber su funcionamiento interno , es mejor utilizar métodos que no impliquen el desarrollo de su física – matemática de modelamiento , es por ello que existen métodos de identificación que nos facilitan la labor cuando nos vemos en la necesidad de usarlos , si bien no es del todo exacto a diferencia del modelo matemático físico , nos da una representación fiel a las características del sistema y por tanto son de importancia cuando se presenta las dificultades descritas. Veremos en el transcurso de la guía que unos sistemas se aproximaran más que otro. Asimismo, podremos calcular el error que existe entre la y(t) aproximada usando cualquier método y la y(t) producto de la gráfica. Los sistemas en algunos casos presentan desplazamientos en el tiempo que influyen en la y(t), para estos sistemas también es posible aplicar los mismos métodos de identificación siempre y cuando hagamos algunas modificaciones. Sabemos que los sistemas de primer orden y segundo orden sobreamortiguado tienen una señal de respuesta al escalón muy parecida. De la misma manera ocurre lo mismo con sus métodos de identificación. En esta guía analizamos los distintos métodos de identificación de sistemas aplicadas a distintos sistemas. Como no existe un único método con el cual generar y(t) aproximado podemos intentar hallar la aproximación de muchas formas.
II. MARCO TEORICO
A partir de la información de la entrada y salida, se puede establecer si el sistema es de primer orden o bien de segundo orden o mayor, además de establecer si existe un retardo o alguna otra característica en particular. Existen muchos métodos para la identificación de un sistema. En este apartado estudiaremos nombraremos a 6 de estos (los cuales han sido usados para elaborar el procedimiento de esta guía).
Para los sistemas de primer orden
Modelo de Alfaro primer orden más tiempo muerto
Las ecuaciones que dan originan los parámetros de importancia para poder construir el sistema son:
Donde
Método de primer orden sin retraso
El modelo propuesto para la identificación de un sistema es:
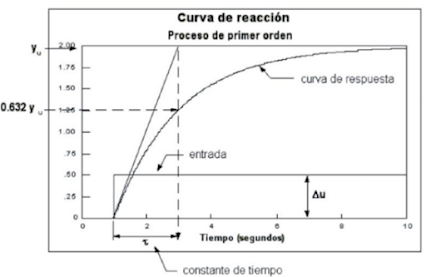
constante de tiempo τ se calcula de acuerdo a la Fig 1.
determinando el tiempo en el que la respuesta del sistema alcanza el 0.632 del valor final de la respuesta.
Figura 1. Método para calcular un modelo de primer orden
Para los sistemas subamortiguados
Método tradicional a partir de la respuesta al escalón [1]
De la respuesta fraccional se obtienen 3 magnitudes (ver figura 2)
Figura 2. Respuesta de un sistema subamortiguado ante una entrada escalón
El coeficiente de amortiguamiento puede estimarse a partir de la expresión de primer sobrevalor:
Segundo método para un sistema de segundo orden subamortiguado
En un sistema de segundo orden sub amortiguado se pueden medir de la respuesta directamente los parámetros generales (su ganancia k, su factor de amortiguamiento ξ y su frecuencia natural ωn). Por lo que se puede ajustar al siguiente modelo:
Figura 3. Método para calcular un modelo de segundo orden subamortiguado
Para los sistemas sobreamortiguados o críticamente amortiguados:
Método de los 2 puntos de Smith [2]
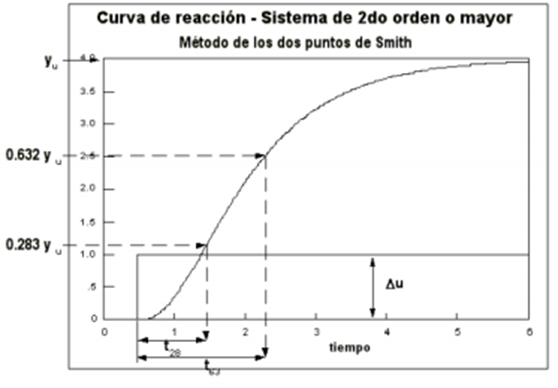
El primer método basado en dos puntos sobre la curva de reacción fue propuesto por Smith. Los instantes seleccionados por este autor fueron los tiempos requeridos para que la respuesta alcance el 28.3% (t_28) y el 63.2% (t_63) del valor final, y corresponden a:
t_28=t_m+τ/3 (13)
t_63=t_m+τ (14)
Este sistema de ecuaciones se puede resolver para tm y τ obteniéndose:
τ=1.5(t_63-t_28) (15)
t_m=t_63-τ (16)
La ganancia del modelo se calcula como en los métodos anteriores:
k=y_u/∆u (17)
Figura 4. Método de Smith
III. MATERIALES Y METODOS
A. EQUIPOS, MATERIALES Y HERRAMIENTAS UTILIZADAS

Figura 5. Software Matlab
Figura 6. Software Simulink
B. ESQUEMAS
Figura 7. Respuesta temporal del sistema 1
Figura 8. Respuesta Temporal del sistema 2
Figura 9. Diagrama del circuito implementado en Proteus
C. PROCEDIMIENTO
a. Parte I: Métodos basados en la curva de reacción
En esta parte identificaremos un modelo para 2 sistemas implementados en Proteus, aplicando los métodos basados en la curva de reacción usando Matlab.
i. Ejecute el Ejecute el programa Proteus y abra el archivo Sistema1.pdsprj. Este archivo contiene un bloque denominado Sistema1.
Figura 10. Diagrama del sistema 1
ii. La respuesta del sistema lo podemos observar en el visor de ‘Analogue Analysis’, tal como se muestra en la siguiente figura.
Figura 11. Respuesta temporal del sistema
iii. Indique de que orden es el sistema a analizar.
A simple vista podemos decir que el sistema, con solo ver la Figura 11 que es de primer orden, pero también podría ser de 2 orden sobreamortiguado, pero descartamos la segunda opción debido a que la respuesta no presenta punto de inflexión cuando empieza su ascensión en magnitud, también notamos que el sistema se estabiliza en un valor cuando la entrada es acotada, además la respuesta no presenta retardo.
iv. Elija el método basado en la de Curva de Reacción, más adecuado según su criterio, para identificar un modelo G(s).
Debido lo dicho en el anterior apartado, nuestro sistema es de primer orden y no presenta retraso para elegimos el modelo para sistemas de primer orden sin retraso, que está definido por la ec(18).
G(s)=k/(τs+1) (18)
Podemos calcular sus parámetros mediante la observación de la Figura 8 en donde determinamos los valores:
- y_u=5
- Δu=5
Hallamos la ganancia por medio de la ec(18)
k=y_u/Δu=1 (19)
El siguiente paso es hallar el τ mediante la grafica tenemos que fijarnos un punto en donde la magnitud es el 63.2% de la magnitud máxima de la respuesta, luego para un determinado tiempo se obtiene ese punto, en donde ese tiempo es nuestro τ.
Para lo cual τ vale 225 ms tenemos el 63.2% de la magnitud máxima. Entonces reemplazando en la ec(18) obtenemos nuestra función transferencia.
G(s)=1/(0.225s+1) (20)
v. Para un mejor análisis y poder comparar la respuesta del modelo hallado con la respuesta del sistema, se utilizará el software MATLAB®.Para ello, exporte los datos haciendo clic en la opción Graph →Export Graph Data ilustración 3 Guarde el archivo con el nombre “Sistema1.dat” en la carpeta que se tiene como directorio MATLAB.
Figura 12. Opción para exportar datos Proteus
vi. En MATLAB®, ejecute la función “proteus2matlab”, utilizando la siguiente sintaxis:
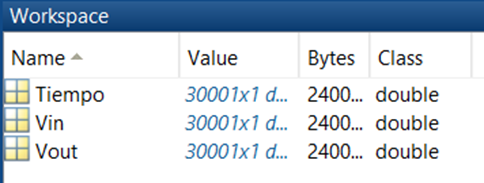
Lo cual creará en el Workspace los vectores Tiempo, Vin y Vout obtenidos a partir del archivo exportado en el punto v.
Figura 13. Comando para exportar datos generados por el comando al workspace
Figura 14. Datos generados por el comando
vii. Grafique los vectores Vin y Vout vs el vector Tiempo. Verifique que sea la misma respuesta obtenida en Proteus.
Utilizando el comando “save” generamos un archivo.mat de nombre “sys.mat” que contiene los datos que se observan en la Fig. 14, ahora crearemos un script en donde lo primero que haremos será cargar los datos con el comando “load sys.mat” , el script generado se guardó en el archivo de nombre : ”sistemaexportado.m” y se muestra en la Fig. 15.
Figura 15. Script que carga y genera las grafica de respuesta del sistema y su entrada
Efectivamente el grafico generado corresponde a lo que se muestra en Proteus, es decir es idéntico a la Figura 11, podemos ver el resultado del Script en la Figura 16.
Figura 16. Comparación entre las gráficas de Matlab y Proteus
viii. Utilice Matlab para hallar un modelo según el método elegido en el punto iv (Cree un script que obtengan los parámetros necesarios)
En base al Script presentado en la Fig. 15, añadiremos líneas de código para hallar sus parámetros , con la ayuda del comando “(end)” podemos obtener el valor final tanto de y_u(“y_est”) y Δu(“u_est”) , luego podemos calcular el valor de K , posteriormente para hallar el valor de tiempo que genera el 63.2% del voltaje máximo utilizamos el comando “find” para buscar un valor cercano o igual a dicha magnitud . Una vez obtenido este dato simplemente procedemos a extraer el instante de tiempo para ese valor como se muestra en la Fig.17
Figura 17. Script que identifica los parámetros del sistema de 1° orden
ix. Defina la función de transferencia, G(s), del modelo obtenido en el paso previo.
Esta función la definiremos en el mismo Script que usamos y lo compararemos con el resultado de identificación obtenido en el anterior apartado inicial. Finalmente definidos nuestras constantes reemplazamos los datos en la ec (18) mediante el comando “tf” y “step” , definimos y ploteamos los resultados para compararlos como se muestra en la Figura 19
Figura 18. Script generador del grafico por identificación
x. Obtenga su respuesta temporal ante una entrada escalón.
Figura 19. Comparativa de la identificación y respuesta obtenida mediante datos del Proteus
Como podemos notar los resultados son bastante similares, ya que superponiéndolos es casi imperceptible ver 2 graficas distintas es por ello que se optó por ponerlas por separado , este proceso se guardado en el mismo Script de nombre “sistemaexportado.m”, en el siguiente apartado veremos las 2 graficas en una sola ventana.
xi. Presente en una sola gráfica, tanto la respuesta temporal obtenida en el punto anterior como la respuesta importada desde Proteus.
Figura 20. Graficas superpuestas
Como se nota en la Figura 20, la similitud es bastante alta conduciendo a que el modelo de identificación es efectivo para este sistema.
xii. A partir del punto anterior, considera que es aceptable la respuesta del modelo obtenido G(s). Justifique su respuesta. (Puede utilizar algunos índices de desempeño como la suma del error cuadrático)
La respuesta como detallamos en el anterior aparte es muy aceptable debido a que las gráficas son muy similares, esto podemos dilucidar haciendo zoom al gráfico, como también hallando el error cuadrático, en la ilustración 22 se muestra un acercamiento para notar que las gráficas no son iguales del todo, en la Fig.21 se muestra parte del Script que nos ayudara a calcular el índice de error y el error medio entre estas 2 graficas.
Figura 21. Comandos para hallar el indicador y el error
Figura 22. Acercamiento de las gráficas, yout aproximado (rojo), yout real (azul)
xiii. Ejecute el programa Proteus y abra el archivo Sistema2.pdsprj. Este archivo contiene un bloque denominado Sistema2.
Figura 23. Diagrama del sistema 2
xiv. La respuesta del sistema lo podemos observar en el visor de ‘Analogue Analysis’, tal como se muestra en la siguiente figura.
Figura 24. Respuesta Temporal del sistema 2
xv. Repita los pasos del iii al xii.( Además de seleccionar alguno de los métodos presentados, investigue de otro método de identificación y también aplíquelo)
iii.2. Indique de que orden es el sistema a analizar.
Resp. Por el comportamiento inicial de la señal de salida (la ligera subida) y por la inflexión que se muestra antes de estabilizarse, podemos decir que el sistema es de segundo orden.
iv.2. Elija el método basado en la de Curva de Reacción, más adecuado según su criterio, para identificar un modelo G(s).
Usaremos el método de los 2 puntos de Smith. Este método te permite hacer una identificación del sistema hallando 2 puntos de la gráfica, construyendo una recta, y a partir de ello hallar los parámetros requeridos. No implica gran complejidad en el procedimiento.
Hallando t_63:
Si la gráfica se encuentra en 5*0.632=3.16 -----> t_63=0.7913
Hallando t_28:
Si la gráfica se encuentra en 5*0.283=1.415 -----> t_28=0.3855
t_63=0.7913 (21)
t_28=0.3855 (22)
τ=1.5*(t_63-t_28) (23)
t_m=t_63- τ (24)
y_u=5 (25)
∆u=5 (26)
k=y_u/∆u (27)
Hallamos G(s):
G(s)=(ke^(-t_m s))/(τs+1) (28)
Ahora hallamos Y(s):
Y(s)=G(s)*X(s) y X(s)=5/s (29)
Y(s)=G(s)x 5/s (30)
v.2. Para un mejor análisis y poder comparar la respuesta del modelo hallado con la respuesta del sistema, se utilizará el software MATLAB®. Para ello, exporte los datos haciendo clic en la opción Graph →Export Graph Data (Fig.12). Guarde el archivo con el nombre “Sistema2.dat” en la carpeta que se tiene como directorio MATLAB®.
Figura 25. El archivo “Sistema.dat” ya se encuentra instalado en la carpeta donde haremos correr Matlab
vi.2. En MATLAB®, ejecute la función “proteus2matlab”, utilizando la siguiente sintaxis:
>>[Tiempo,Vin,Vout]=
proteus2matlab('Sistema2.dat);
Lo cual creará en el Workspace los vectores Tiempo, Vin y Vout obtenidos a partir del archivo exportado en el punto v.
Figura 26. Se ejecuta ahora la función que se ve en la figura
Figura 27. Se guardan los valores Tiempo, Vin y Vouten el Workspace
vii.2. Grafique los vectores Vin y Vout vs el vector Tiempo. Verifique que sea la misma respuesta obtenida en Proteus.
Figura 28. Confirmamos que la gráfica obtenida en Matlab es la misma que obtuvimos en Proteus
viii.2. Utilice Matlab para hallar un modelo según el método elegido en el punto iv. (Cree un script que obtengan los parámetros necesarios).
Para el análisis en Matlab hemos realizado 2 códigos (primera y segunda forma) que tendrán el mismo objetivo (hallar “Vout(t)” y “Vout(t) aproximado”). La primera forma se hará a partir del ejemplo realizado en clase, mientras que la segunda forma se realizará usando variables simbólicas y la función ilaplace.
Primera forma de hallar y(t) aproximado (método enseñado en la clase):
Figura 29. Script que identifica los parámetros del sistema de 1° orden (primera forma)
Segunda forma de hallar y(t) aproximado usando variable symbolic e ilaplace:
Figura 30. Se muestra el código que hemos usado para hallar los parámetros del sistema (segunda forma)
ix.2. Defina la función de transferencia, G(s), del modelo obtenido en el paso previo.
Figura 31. Defino G(s) a partir de los parámetros obtenidos (primera forma), el desplazamiento será introducido después.
Figura 32. Defino G(s) a partir de los parámetros obtenidos (segunda forma)
x.2. Obtenga su respuesta temporal ante una entrada escalón.
Figura 33. y(t) obtenida a partir de Y(s)=G(s)* X(s) y aplicando transformada de fourier inversa (primera forma), notese que yout realiza un corrimiento para añadir el restraso tm (punto 1828)
Figura 34. y(t) obtenida a partir de Y(s)=G(s)* X(s) y aplicando transformada de fourier inversa (segunda forma)
xi.2. Presente en una sola gráfica, tanto la respuesta temporal obtenida en el punto anterior como la respuesta importada desde Proteus.
Figura 35. Se muestra las 2 graficas: y(t) en color rojo (salida del sistema) y “y(t)” aproximado obtenido a través del método Smith en color azul (primera forma)
Figura 36. Se muestra las 3 graficas: 5*u(t) en color azul (entrada del sistema), y(t) en color rojo (salida del sistema) y “y(t)” aproximado obtenido a través del método Smith en color verde (segunda forma)
xii.2. A partir del punto anterior, considera que es aceptable la respuesta del modelo obtenido G(s). Justifique su respuesta. (Puede utilizar algunos índices de desempeño como la suma del error cuadrático)
Ciertamente consideramos que la función G(s) Obtenida es aceptable. Ya que se puede ver que hay muy poco margen de error en la etapa transitoria del sistema. Para corroborar esto usamos la suma del error cuadrático medio en 10 puntos de la etapa transitoria entre 0 a 3. De esa manera comprobaremos lo que hemos dicho:
Error cuadrático:
Figura 37. Error cuadrático de la función aproximada. también se muestra el valor del indicador dividido entre la cantidad de muestras, como se puede ver es bastante pequeño
Figura 38. Se muestra la diferencia entre y(t) (en rojo) y y(t) aproximado (en azul)
Error cuadrático medio:
Para calcular el error medio cuadrático escogeremos 11 puntos (entre 0 y 3), aplicaremos la fórmula del error medio cuadrático y analizaremos el valor que nos quede:
i = número de punto
t = valor en el tiempo
y(t) = señal de respuesta
y’(t) = señal de respuesta aproximada
ri = y(t)- y’(t)
Tabla 1. Cuadro comparativo
- Comprobamos que el error medio cuadrático entre y(t) y y(t) aproximada es muy bajo. Por lo que podemos concluir que la aproximación ha sido bastante acertada.
Aplicación de un segundo método: Método de los 2 puntos General [3]
Con posterioridad a la presentación del método de dos puntos de Smith se han desarrollado otros basados en el mismo procedimiento, diferenciándose únicamente en la selección de los dos instantes en que la respuesta del modelo se hace coincidir con la del proceso real.
Pueden establecerse, por consiguiente, ecuaciones generales para los métodos de dos puntos, con el fin de identificar un modelo de primer orden más tiempo muerto dado por (1) con base en los tiempos requeridos para alcanzar dos puntos específicos en la curva de reacción del proceso.
Si p1 y p2 son dos valores porcentuales del cambio en la respuesta del sistema a un cambio escalón en la entrada y t1 y2 son los tiempos requeridos para alcanzar estos dos valores, como se muestra en la Fig. 39. entonces los parámetros de un modelo de primer orden más tiempo muerto se pueden obtener de:
τ=at_1+bt_2 (34)
t_m=ct_1+dt_2 (35)
Figura 39. Métodos de 2 puntos
Tabla 2. Constantes para la identificación de los métodos
Para este caso tomaremos el método de Alfaro, de Broida y método de Cheng y Yang:
Método de Alfaro:
t_75=1.0025 (36)
t_25=0.3525 (37)
τ=0.91t_75-0.91t_25=0.5925 (38)
t_m=-0.262t_75+1.262t_25=0.1822 (39)
y_u=5 (40)
∆u=5 (41)
k=y_u/∆u=1 (42)
G(s)=e^(-0.1822s)/(0.5925s+1) (43)
Figura 40. Script para plotear y(t) aproximado a través del método de Alfaro
Método de Broide:
t_40=0.5054 (44)
t_28=0.3825 (45)
τ=5.5t_40-5.5t_28=0.6759 (46)
t_m=-1.8t_40+2.8t_28=0.1613 (47)
y_u=5 (48)
∆u=5 (49)
k=y_u/∆u=1 (50)
G(s)=e^(-0.1613s)/(0.6759s+1) (51)
Figura 41. Script para plotear y(t) aproximado a través del método de Broide
Método de Cheng y Yang:
t_67=0.8508 (52)
t_33=0.4329 (53)
τ=1.4t_67-1.4t_33=0.5851 (54)
t_m=-0.54t_67+1.54t_33=0.2072 (55)
y_u=5 (56)
∆u=5 (57)
k=y_u/∆u=1 (58)
G(s)=e^(-0.2072s)/(0.5851s+1) (59)
Figura 42. Script para plotear y(t) aproximado a través del método de Cheng y Yang
Plotemos ahora las señales:
Figura 43. Ploteamos la señal escalón de entrada y la señal de salida y(t) (color azul y rojo respectivamente)
Figura 44. Ploteamos la señal y(t) aproximado con el método de Alfaro (color verde), y(t) aproximado con el método de Broide (color verde), y(t) aproximado con el método de Cheng yYang (color azul claro)
Figura 45. Se muestran las gráficas producto de usar los 3 métodos
Análisis:
Hemos graficado la función aproximada con 3 métodos distintos para poder saber cuál de estas es la que más se parece a la función real. Viendo la gráfica podemos decir que los 3 métodos presentan unas funciones aproximadas parecidas, ya que solo es cuestión de variar los puntos t1 y t2. A simple vista se observa que el método más aproximado es el de Alfaro, seguido por el de Cheng y Yang, y finalmente el método el método de Broide.
Calculo de error cuadrático medio con estos 3 métodos:
Para hallar el error cuadrático medio de los 3 métodos con respecto al Vout real debemos usar la función “immse()” primero debemos cortar Vout, ya que este tiene una longitud de 50001 puntos y Vout aproximado (ynum) tiene una longitud de 501 puntos. Mientras que el Vout aproximado contiene 501 elementos. Además, Vout aproximado (le pusimos como variable ynum) es una variable simbolica, para hallar el error medio cuadrático primero lo debemos convertir a doublé. Nos dimos cuenta que Vout es un vector vertical, y ynum es un vector horizontal. Por eso, para operar e error cuadrático medio usamos la transpuesta de Vout .
|
i |
t |
y(t) |
y’(t) |
ri |
ri2 |
|
1 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0.3 |
0.9928 |
0.8771 |
0.1157 |
0.0134 |
|
3 |
0.6 |
2.427 |
2.481 |
-0.054 |
0.0029 |
|
4 |
0.9 |
3.496 |
3.461 |
0.035 |
0.0012 |
|
5 |
1.2 |
4.159 |
4.06 |
0.099 |
0.0098 |
|
6 |
1.5 |
4.537 |
4.426 |
0.111 |
0.0123 |
|
7 |
1.8 |
4.747 |
4.649 |
0.098 |
0.0096 |
|
8 |
2.1 |
4.864 |
4.786 |
0.078 |
0.0061 |
|
9 |
2.4 |
4.928 |
4.869 |
0.059 |
0.0035 |
|
10 |
2.7 |
4.963 |
4.92 |
0.043 |
0.0018 |
|
11 |
3.0 |
4.984 |
4.951 |
0.033 |
0.0011 |














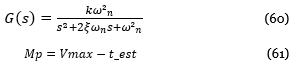








Figura 46. Calculo del error cuadrático de los 3 métodos usados
Figura 47. Resultados del error cuadrático medio usando los 3 métodos
Tal y como lo vimos a través de la gráfica, el método de Alfaro es el más cercano al Vout real, ya que presenta menor error cuadrático medio, seguido por el método de Cheng y Yang y el método de Broide.
b. Parte II: Identificación de un sistema físico
i. Implemente el circuito presentado en la siguiente figura.
Figura 48. Diagrama del circuito implementado en Proteus
ii. Conecte una señal de entrada adecuada que permita observar la curva de reacción de sistema.
La señal de entrada será un escalón de amplitud 1V que se logra apreciar en la Figura 47, la gráfica de color rojo que es Vin y el verde Vout .
Figura 49. Respuesta temporal del sistema ante un escalón
iii. Utilizando uno de los métodos de identificación presentados, el más adecuado según su criterio, obtenga un modelo para el circuito implementado. Compare este modelo con el obtenido en su informe previo.
Utilizando el modelo para sistemas subamortiguados de 2 orden, para definir nuestra función transferencia debemos conocer sus parámetros para ello lo primero que haremos será exportar los datos de la gráfica de la Figura 47, escribir el comando en Matlab para entrar los 3 vectores de Vin , Vout, Tiempo , con la función:
Figura 50. Comando para extraer datos
Una vez extraídos los datos procederemos a guardar lo datos del workspace con el comando “save ('sys3.mat')”, Luego crearemos un Script de nombre “identificacionSistema3.m” el cual su primera parte constara del respectivo grafico visto en proteus, como se muestra en la figura 49, la gráfica del sistema se muestra en la figura 50.
Figura 51. Script que carga y genera las grafica de respuesta del sistema y su entrada
Figura 52. Resultado del Script
Luego de plotear la gráfica de respuesta mostrada en la fig. 50, ahora hallaremos sus parámetros según el modelo que está definido en la ec(60) , primero hallamos el valor de tp usado el comando “max” para obtener el voltaje(V) máximo de la gráfica que represente el valor del sobrepico , en donde tp será el valor para cuando la respuesta en voltaje sea la más alta, posteriormente se calcula Mp con la ec(61),añadiremos líneas de código en el Script que se muestra en la Figura 51.
Figura 53. Script que halla el parámetro Mp y Tp
Una vez obtenido el parámetro Mp y tp es posible hallar el factor de amortiguamiento ξ resolviendo la ec(62).
Mp=e^(-ξπ/√(1-ξ²)) (62)
Haciendo un poco calculo podemos despejar ξ como se muestra en la ec(63) , también podemos hallar ω_n con la ec(64).
Todas las ecuaciones lo definimos en el Script de Matlab y se muestra en la Figura 52
Figura 54. Script que halla los parámetros del sistema
Una vez obtenidos ω_n y ξ ahora podemos describir el sistema adecuadamente mediante la ec(60) , posteriormente solo debemos describir esta ecuación en el Script y reemplazar sus valores para finalmente plotearlo y comparar los resultados que son apreciables en la figura 54, Finalmente se hace uso del comando “immse” para ver el error medio cuadrático existente.
Figura 55. Script que integra los parámetros en la función transferencia del sistema
Figura 56. Respuesta generada por identificación
Si observamos mejor y comparamos la Figura 56 que generamos a partir de la identificación y la Figura 52 que es la respuesta del sistema, notaremos que ambos son muy similares , pero con algunas diferencias que son apreciables por muy poco pero que ambas tienen características similares como por ejemplo el valor de sobrepico y el valor donde la amplitud se vuelve estable , como también los 2 sobre impulsos al alcanzar la estabilidad de amplitud. Con respecto al parámetro hallado Mp (sobreelongacion)hay que tener cuidado cuando la señal de excitación no es de magnitud 1, por ello utilizamos la formula general debido a que si cometemos una equivocación en el Parámetro de sobreelongacion , el factor de amortiguamiento que depende de este ,no coincidirá con la gráfica del sistema obtenida en Proteus.
iv. Investigue de otro método de identificación y aplíquelo.
Usaremos el método tradicional a partir de la respuesta al escalón:
Método tradicional a partir de la respuesta al escalón
De la respuesta fraccional se obtienen 3 magnitudes (ver figura 57)
Figura 57. Respuesta de un sistema subamortiguado ante una entrada escalón
v. Defina en Matlab los modelos hallados en los puntos iii y iv.
Figura 58. Cargamos sysprueba.dat
Primero cargamos y ploteamos los vectores guardados en sys3,dat. Aquí se encuentran contenidos el Vin y el Vout del sistema a identificar.
Figura 59. Hallamos los parámetros Sv1 y Sv2
La primera parte de este método de identificación es hallar SV1, esto lo consequimos primero obteniendo Vmax, y depues el tiempo estacionario del sistema, la resta de estos 2 me da como resultado SV1.
El SV2 es parecido, pero ahora tenmos que hallar Vmax sin conta con el Vmax más grande, por eso hacemos un recorte de la gráfica en el punto 15, (antes del punto 15 ocurrió la primera Vmax), por lo que después del recorte hallara el Vmax2.
Ya con el el Sv2 y Sv1 halladas procedemos a calcular el RA (relación de atenuación. Como el épsilon es hallado a través de RA, hallamos el épsilon.
Figura 60. Hallamos los parámetros tp, wn y ξ
Calculamos también el tp1 y el tp2. Para el tp1 hallamos el índice del tiempo cuando Vout es máxima (la sobreelongacion).
Para el tp2 hallamos el tiempo cuando Vout es máxima. Pero como hicimos un recorte en el punto 15. Le tenemos que sumar el tiempo anterior (Tiempo(14)), de esa forma hallamos el tp2.
Solo nos queda ahora restar tp2-tp1 para hallar tp.
A partir de esto hallamos el wp. Seguidamente podemos hallar wn de wp y épsilon. De esta manera tendremos todos los parámetros para halar elG(s)
Figura 61. Hallamos G(s)
Como ya hallamos el G(s) y tenemos una entrada escalón por 5. Definimos en el step esa entrada y ploteamos el yout con el tout para hallar la señal Vout aproximada.
vi. Compare las respuestas temporales obtenidas en Matlab con la del circuito implementado.
Comparación:
Figura 62. Se muestra la respuesta Vout en la salida del circuito (color azul), y Vout aproximado (color morado)
Observamos que la Vout(t) y la Vout(t) aproximada son muy parecidas, en donde existe una diferencia es en la sobreelongación, mientras que Vout(t) apenas sobrepasa los 6v, el Vout(t) aproximado pasa con más holgura los 6 v. También existe un tiempo de diferencia en las sobreelongaciones. El segundo pico en la Vout(t) aproximada ocurre antes que en la Vout(t). Por lo demás vemos que sigue el mismo comportamiento que el de la original. Podemos decir que la aproximación con este método ha sido bastante buena.
Podemos hallar ahora el error cuadrático para comprobar que el sistema aproximado está bastante acertado:
Figura 63. Error cuadrático para el caso del sistema de la figura 62
vii. ¿Cuál de los dos modelos representa mejor al circuito implementado? Justifique su respuesta.
Por las características mostradas y analizando la respuesta aproximada que obtuvimos con los 2 métodos, podemos decir que el método 2 representa mejor al circuito implementado, el análisis matemático en ambos es parecido. Pero en el segundo método trabajamos con relación de atenuación, ósea, con la sobreelongación y además con el otro pico más alto. Al involucrar más valores de la gráfica real estamos obteniendo una mejor representación. Podemos observar además el bajo error cuadrático que existe en el segundo método. Con esto comprobamos que este método creara una Vout(t) aproximada muy parecida a la Vout(t) real.
III. CONCLUSIONES:
-A La identificación de sistemas es de mucha utilidad cuando se quiere modelar la función de transferencia de un sistema
- La identificación representa modelos que se aproximan al modelo real de un sistema
- Algunos métodos de identificación son para casos específicos por lo tanto antes de realizarlo debemos conocer las características del sistema
- No hay un solo método de identificación de sistemas para un tipo de sistema en particular. Por lo tanto, debemos escoger el sistema que más se aproxime al sistema real.
- Para saber que tan exacto es el sistema aproximado que hemos hallado debemos hallar el error cuadrático del sistema, también se le podría hallar el error cuadrático medio, o hacer un zoom a la gráfica y comparar la distancia entre estas
- Los sistemas aproximados que más se parecieron a los reales son los de primer orden y segundo orden sobreamortiguados. En los casos de sistemas subamortiguados se presentaban desaciertos en la sobreelongacion. Esto lo hacía más difícil de identificar.
IV. REFERENCIAS
[1]:https://catedras.facet.unt.edu.ar/controldeprocesos/wp-content/uploads/sites/85/2016/02/Tp2a.pdf (pag.3)
[2]:https://www.researchgate.net/profile/Victor_Alfaro/publication/260058479_Identificacion_de_procesos_sobreamortiguados_utilizando_tecnicas_de_lazo_cerrado/links/0deec52f3b83b6011c000000/Identificacion-de-procesos-sobreamortiguados-utilizando-tecnicas-de-lazo-cerrado.pdf (pag. 6)
[3]:https://www.researchgate.net/profile/Victor_Alfaro/publication/260058479_Identificacion_de_procesos_sobreamortiguados_utilizando_tecnicas_de_lazo_cerrado/links/0deec52f3b83b6011c000000/Identificacion-de-procesos-sobreamortiguados-utilizando-tecnicas-de-lazo-cerrado.pdf (pag. 8)
[4]: Ingeniería de control moderna – Ogata (capitulo 5: Análisis de las respuestas transitorias y estacionarias)