Autor: Mauro Benito Montoya Arenas (mauro2017pre@gmail.com)

Laboratorio N°7: “Diseño para testabilidad: modelo stuck-at 0 - stuck-at 1”

RESUMEN:

En este laboratorio analizamos las fallas stuck at 0 y stuck at 1 en el circuito comparador y comparador con entradas complemento a 2 del laboratorio 5. Primero contamos el número de líneas del circuito, después hallamos el conjunto mínimo de vectores de test para una cobertura del 100%. Después, detectamos si existe alguna falla que no pueda ser testeada. Para finalizar, introducimos 2 fallos stuck at 0 y 2 fallos stuck at 1 en el comparador y simulamos. Todas las conclusiones obtenidas se encuentran en el final del informe.

INTRODUCCION:

Las fallas atascadas (stuck-at) ocurren cuando una línea está pegada permanentemente a Vdd o a tierra dando una salida defectuosa. Esta línea puede ser una entrada o salida a cualquier puerta. Además, esta falla puede ser única o múltiples. Cuando una señal, o salida de puerta, se atasca en un valor de 0 o 1, independientemente de las entradas al circuito, se dice que la señal está "atascada" y el modelo de falla utilizado para describir este tipo de error se denomina "atascado”. Los modelos básicos de fallas en circuitos digitales incluyen el modelo de falla atascada, el modelo de falla puente, las fallas de transistor, el modelo de falla abierta, el modelo de falla de retardo, etc. En las últimas décadas, el modelo de falla más popular utilizado en la práctica es el modelo único atascado en la falla. Para usar este modelo de falla, se asume que cada pin de entrada en cada puerta a su vez está conectado a tierra o a Vdd, y se desarrolla un vector de prueba para indicar que el circuito está defectuoso. Por lo tanto, si un circuito tiene n líneas de señal, hay potencialmente 2n fallas atascadas definidas en el circuito.

OBJETIVOS:

Ø Hacer las simulaciones de todas las fallas posibles stuck-at 0 y stuck-at 1 del circuito.

Ø Aprender el funcionamiento del modelo del stuck-at o y stuck-at 1 para detectar falas.

Ø Detallar y describir la nueva salida del circuito debido a alguna falla provocada en una línea

TEMA PROPUESTO:

Laboratorio N°7: “Diseño para testabilidad: modelo stuck-at 0 - stuck-at 1”

BASES TEORICAS:

a) Marco Teórico:

Compuertas Lógicas:

Las compuertas lógicas son dispositivos que operan con aquellos estados lógicos que funcionan igual que una calculadora, de un lado ingresas los datos, ésta realiza una operación, y finalmente, te muestra el resultado.

Figura 1. Diagrama de bloque que representa una compuerta lógica

Cada una de las compuertas lógicas se las representa mediante un Símbolo, y la operación que realiza (Operación lógica) le corresponde una tabla, llamada Tabla de Verdad.

Figura 2. Compuerta de not y su tabla de la verdad

Figura 3. Compuerta de or y su tabla de la verdad

Figura 4. Compuerta de or y su tabla de la verdad

Stuck at

Una falla atascada (falla stuck-at) es un modelo de falla particular utilizado por simuladores de fallas y herramientas de generación automática de patrones de prueba para imitar un defecto de fabricación dentro de un circuito integrado. Se supone que las señales y los pines individuales están atascados en '1' lógico (stuck-at 1) o '0' lógico (stuck-at 0). Por ejemplo, una entrada está vinculada a un estado lógico 1 durante la generación de la prueba para asegurar que se pueda encontrar un defecto de fabricación con ese tipo de comportamiento con un patrón de prueba específico. Asimismo, la entrada podría vincularse a un 0 lógico para modelar el comportamiento de un circuito defectuoso que no puede cambiar su pin de salida. No todas las fallas pueden analizarse utilizando el modelo de falla atascada. La compensación de los peligros estáticos, es decir, las señales de derivación, puede hacer que un circuito no sea comprobable con este modelo. Además, los circuitos redundantes no se pueden probar con este modelo, ya que por diseño no hay cambios en ninguna salida como resultado de una sola falla.

Figura 5. Ejemplo de fallos stuck at 0 (izquierda) y atuck at 1 (derecha)

Marco conceptual:

Software DSCH:

Descripción:

El programa DSCH es un editor y simulador lógico. DSCH se utiliza para validar la arquitectura del circuito lógico antes de que se inicie el diseño microelectrónico. DSCH proporciona un entorno fácil de usar para el diseño de lógica jerárquica y una simulación rápida con análisis de retardo, que permite el diseño y validación de estructuras lógicas complejas.

DSCH también incluye los símbolos, modelos y soporte de montaje para los controladores 8051 y PIC16F84. Los diseñadores pueden crear circuitos lógicos para interactuar con estos controladores y verificar los programas de software usando DSCH.

Características:

- Entorno amigable para el usuario para el diseño rápido de circuitos lógicos.

- Admite el diseño de lógica jerárquica.

- Se agregó una herramienta sobre análisis de fallas a nivel de puerta de digital. Fallos: atascado en 1, atascado en 0. La técnica permite la inyección de una sola falla atascada en los nodos del circuito.

- Interfaz mejorada entre DSCH y Winspice.

- Maneja tanto la simulación lógica convencional basada en patrones como la simulación intuitiva en pantalla manejada por el mouse.

- Extractor incorporado que genera una lista de redes SPICE a partir del diagrama esquemático

(Compatible con PSPICETM y WinSpiceTM).

- Genera una descripción VERILOG del esquema para la conversión del diseño.

- Acceso inmediato a las propiedades del símbolo (Delay, fanout).

- Soporte de modelo y montaje para microcontroladores 8051 y PIC 16F84.

- Soporte de tecnología submicrónica, submicrónica profunda y nanoescala.

- Apoyado por una enorme biblioteca de símbolos

Figura 6. Multiplexor 74ls138 hecho con el software DSCH

DESARROLLO DEL TRABAJO:

I) De las siguientes preguntas del Laboratorio N° 5: B, C

Elegir 01 (UNA) pregunta considerando las indicaciones dadas en cada pregunta. Adicionalmente se puede reducir el diseño a 3X3 bits. Se pide:

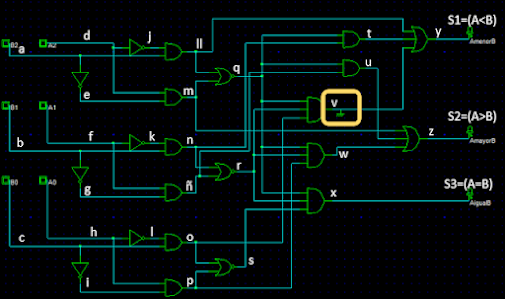
a) Determinar el número total de líneas del circuito que pueden tener los fallos S-AT-0 y S-AT-1.

Comparador 3x3 bits

Para el análisis del S-AT0 y S-AT 1, nombramos todas las líneas:

Figura 7. Comparador 3x3 bits

Existe en total 28 líneas. Por lo tanto, pueden existir 56 fallos (28 fallos stuck-at 0 y 28 fallos stuck-at 1)

Comparador 3x3 bits (complemento a 2)

Complemento a 2	Decimal
011	3
010	2
001	1
000	0
111	-1
110	-2
101	-3
100	-4

Tabla 1. Complemento a 2

Para el análisis del S-AT0 y S-AT 1, nombramos todas las líneas:

Figura 8. Comparador 3x3 bits

Existe en total 28 líneas. Por lo tanto, pueden existir 56 fallos (28 fallos stuck-at 0 y 28 fallos stuck-at 1)

b) Hallar el conjunto mínimo de vectores de test para detectar todos los fallos S-AT-0 y fallos S-AT-1.

Comparador 3x3 bits

Stuck-at 0

A2A1A0B2B1B0

ll0

ñ0

000000

011111

101111

110111

100000

010000

001000

111111

Tabla 2. Tabla de fallos stuck at 0

Stuck-at 1

A2A1A0B2B1B0

ll1

ñ1

000000

011111

101111

110111

100000

010000

001000

111111

Tabla 3. Tabla de fallos stuck at 1

Conjunto mínimo de vectores de test:

<A2,A1,A0,B2,B1,B0>=<0,0,0,0,0,0>

<A2,A1,A0,B2,B1,B0>=<0,1,1,1,1,1>

<A2,A1,A0,B2,B1,B0>=<1,0,1,1,1,1>

<A2,A1,A0,B2,B1,B0>=<1,1,0,1,1,1>

<A2,A1,A0,B2,B1,B0>=<1,0,0,0,0,0>

<A2,A1,A0,B2,B1,B0>=<0,1,0,0,0,0>

<A2,A1,A0,B2,B1,B0>=<0,0,1,0,0,0>

<A2,A1,A0,B2,B1,B0>=<1,1,1,1,1,1>

El conjunto mínimo de vectores de test será de 8 vectores

Cobertura alcanzada:

Cobertura alcanzada=(#fallos detectados)/2N x100%=56/56 x100%

Cobertura alcanzada=100%

Comparador 3x3 bits (complemento a 2)

Stuck-at 0

A2A1A0B2B1B0

ll0

ñ0

000000

111011

101111

110111

000100

010000

001000

111111

Tabla 4. Tabla de fallos stuck at 0

Stuck-at 1

A2A1A0B2B1B0

ll1

ñ1

000000

111011

101111

110111

000100

010000

001000

111111

Tabla 5. Tabla de fallos stuck at 1

Conjunto mínimo de vectores de test:

<A2,A1,A0,B2,B1,B0>=<0,0,0,0,0,0>

<A2,A1,A0,B2,B1,B0>=<1,1,1,0,1,1>

<A2,A1,A0,B2,B1,B0>=<1,0,1,1,1,1>

<A2,A1,A0,B2,B1,B0>=<1,1,0,1,1,1>

<A2,A1,A0,B2,B1,B0>=<0,0,0,1,0,0>

<A2,A1,A0,B2,B1,B0>=<0,1,0,0,0,0>

<A2,A1,A0,B2,B1,B0>=<0,0,1,0,0,0>

<A2,A1,A0,B2,B1,B0>=<1,1,1,1,1,1>

El conjunto mínimo de vectores de test será de 8 vectores

Cobertura alcanzada:

Cobertura alcanzada=(#fallos detectados)/2N x100%=56/56 x100%

Cobertura alcanzada=100%

c) Determinar si hay alguna línea del circuito que no es testable.

- En el análisis del comparador 3x3 y comparador complemento a 2 3x3 podemos concluir que no existe ninguna línea que no sea testable.

d) En el programa DSCH (desde el esquemático) simular el circuito con fallo, como mínimo para 02 de vectores de test encontrados en la parte b.

Comparación de 3x3 bits

Stuck-at 0 en la línea k

Figura 9. Stuck-at o en la línea k del comparador 3x3 bits

< A2,A1,A0,B2,B1,B0>=<1,0,1,1,1,1>

Figura 10. Camino de sensibilización

Existe 1 vector de test en el conjunto mínimo

Stuck-at 0 en la línea v

Figura 11. Stuck-at o en la línea v del comparador 3x3 bits

< A2,A1,A0,B2,B1,B0>=<1,1,0,1,1,1>

Figura 12. Camino de sensibilización

Existe 1 vector de test en el conjunto mínimo

Stuck-at 1 en la línea a

Figura 13. Stuck-at 1 en la línea a del comparador 3x3 bits

< A2,A1,A0,B2,B1,B0>=<0,0,0,0,0,0>

Figura 14. Camino de sensibilización

Existe 1 vector de test en el conjunto mínimo

Stuck-at 1 en la línea ll

Figura 15. Stuck-at 1 en la línea a del comparador 3x3 bits

< A2,A1,A0,B2,B1,B0>=<0,0,0,0,0,0>

Figura 16. Camino de sensibilización

< A2,A1,A0,B2,B1,B0>=<1,0,0,0,0,0>

Figura 17. Camino de sensibilización

< A2,A1,A0,B2,B1,B0>=<0,1,0,0,0,0>

Figura 18. Camino de sensibilización

< A2,A1,A0,B2,B1,B0>=<0,0,1,0,0,0>

Figura 19. Camino de sensibilización

Existe 4 vectores de test en el conjunto mínimo

Comparación de 3x3 bits (complemento a 2)

Stuck-at 0 en la línea e

Figura 20. Stuck-at o en la línea e del comparador 3x3 bits complemento a 2

< A2,A1,A0,B2,B1,B0>=<0,0,0,1,0,0>

Figura 21. Camino de sensibilización

- Existe 1 vector de test en el conjunto mínimo

Stuck-at 0 en la línea ñ

Figura 22. Stuck-at o en la línea v del comparador 3x3 bits

< A2,A1,A0,B2,B1,B0>=<0,1,0,0,0,0>

Figura 23. Camino de sensibilización

- Existe 1 vector de test en el conjunto mínimo.

Stuck-at 1 en la línea i

Figura 24. Stuck-at 1 en la línea a del comparador 3x3 bits

< A2,A1,A0,B2,B1,B0>=<1,1,1,1,1,1>

Figura 25. Camino de sensibilización

- Existe 1 vector de test en el conjunto mínimo

Stuck-at 1 en la línea s

Figura 26. Stuck-at 1 en la línea a del comparador 3x3 bits

< A2,A1,A0,B2,B1,B0>=<1,1,0,1,1,1>

Figura 27. Camino de sensibilización

- Existe 1 vector de test en el conjunto mínimo

CONCLUSIONES:

Ø Todas las líneas pueden tener fallos stuck at 0 y stuck at 1. El total de fallos posibles en un circuito será de 2 por el número de líneas.

Ø Para analizar los fallos stuck at 0 y stuck at 1 debemos hallar vectores de test. Con estos vectores analizaremos la salida. Si el circuito no presenta fallas la salida será la esperada, pero si tiene fallas nos saldrá una salida que es distinta.

Ø Para circuitos grandes. La cobertura de la detección de fallos debe ser como mínimo del 95%.

Ø El conjunto mínimo de vectores de test se refiere al conjunto de test suficientes para detectar más del 95% de los fallos de un circuito.

Diseño para testabilidad: modelo stuck-at 0 - stuck-at 1

Laboratorio N°7: “Diseño para testabilidad: modelo stuck-at 0 - stuck-at 1”

Sin comentarios

Artículos populares

Procesamiento digital de señales (ejemplos usando matlab)

¿Como configurar un microcontrolador PIC? - Primer Hola Mundo

PROYECTO: SISTEMA DE TRÁFICO VEHICULAR UTILIZANDO EL PIC 18F4550

¿Qué son los Sistemas embebidos?

Search

Featured post

EDA: Análisis exploratorio de datos de la presion de descarga de pescado en 3 embarcaciones

Labels

Autores

Laboratorio N°7: “Diseño para testabilidad: modelo stuck-at 0 - stuck-at 1”

Entradas que pueden interesarte

Sin comentarios

Artículos populares

Procesamiento digital de señales (ejemplos usando matlab)

¿Como configurar un microcontrolador PIC? - Primer Hola Mundo

PROYECTO: SISTEMA DE TRÁFICO VEHICULAR UTILIZANDO EL PIC 18F4550

¿Qué son los Sistemas embebidos?

Search

Featured post

EDA: Análisis exploratorio de datos de la presion de descarga de pescado en 3 embarcaciones

Labels

Autores