Autor: Mauro Benito Montoya Arenas (mauro2017pre@gmail.com)

ARMONICOS

CONCEPTO:

Los armónicos son frecuencias que son múltiplos enteros de la frecuencia fundamental. La frecuencia fundamental es la frecuencia más baja de una forma de onda periódica.

Ejemplo 1:

Supongamos que tenemos una señal que conectamos al osciloscopio y analizador de espectro para notar su comportamiento:

Figura 1. Función diente de sierra en el tiempo

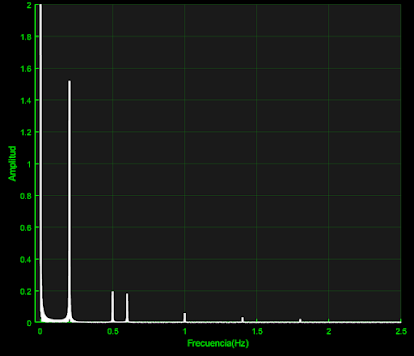
Figura 2. Espectro de la función diente de sierra

Podemos observar que la señal es la función diente de sierra:

f(t)=A/2-A/π sin(wt)-A/2π sin(2wt)-A/3π sin(3wt)-A/4π sin(4wt)-A/5π sin(5wt)-A/6π sin(6wt)-A/7π sin(7wt)…

Observando la función en el dominio del tiempo nos damos cuenta de que A=4 (amplitud) y T=5s -> f=0.2Hz.

Nos falta por determinar la cantidad de armónicos que esta presenta y la amplitud en cada una de estas frecuencias. Analizando su espectro podemos notar que existe:

- Una componente constante: f=0Hz con amplitud=2

- Una componente fundamental: f1=0.2Hz con amplitud=1.27

- 9 armónicos que son múltiplos de la frecuencia fundamental: f2=0.4 Hz con amplitud=0.64, f3=0.6 Hz con amplitud=0.42, f4=0.8 Hz con amplitud=0.32, f5=1 Hz con amplitud=0.25, f6=1.2 Hz con amplitud=0.21, f7=1.4 Hz con amplitud=0.18, f8=1.6 Hz con amplitud=0.16, f9=1.8 Hz con amplitud=0.14 y f10=2 Hz con amplitud=0.13.

La ecuación de la función diente de sierra que vimos en el osciloscopio será la siguiente

f(t)=2-1.27sin(2π0.2t)-0.64sin(2*2π0.2t)-0.42sin(3*2π0.2t)-0.32sin(4*2π0.2t)-0.25sin(5*2π0.2t)-0.21sin(6*2π0.2t)-0.18sin(7*2π0.2t)-0.16sin(8*2π0.2t)-0.14sin(9*2π0.2t)-0.13sin(10*2π0.2t)

Ejemplo 2:

La señal triangular es una señal muy común en electrónica. En este ejemplo analizaremos una señal triangular e identificaremos sus componentes. Como sabemos la señal triangular presenta la siguiente formula:

f(t)=A/2-4A/π^2 cos(wt)-4A/(3π)^2 cos(3wt)-4A/(5π)^2 cos(5wt)-4A/(7π)^2 cos(7wt)-4A/(9π)^2 cos(9wt)-…

La señal triangular observada en el osciloscopio y analizador de espectro es la siguiente:

Figura 3. Función triangulo en el tiempo

Figura 4. Espectro de la función triangulo

Observando la función en el dominio del tiempo nos damos cuenta de que A=4 (amplitud) y T=5s -> f=0.2Hz.

Nos falta por determinar la cantidad de armónicos que esta presenta y la amplitud en cada una de estas frecuencias. Analizando su espectro podemos notar que existe:

- Una componente constante: f=0Hz con amplitud=2

- Una componente fundamental: f1=0.2Hz con amplitud=1.62

- 9 armónicos que son múltiplos de la frecuencia fundamental: f2=0.4 Hz con amplitud=0, f3=0.6 Hz con amplitud=0.18, f4=0.8 Hz con amplitud=0, f5=1 Hz con amplitud=0.06, f6=1.2 Hz con amplitud=0, f7=1.4 Hz con amplitud=0.03, f8=1.6 Hz con amplitud=0, f9=1.8 Hz con amplitud=0.02 y f10=2 Hz con amplitud=0.

La ecuación de la función diente de sierra que vimos en el osciloscopio será la siguiente

f(t)=2-1.62sin(2π0.2t)-0.18sin(3*2π0.2t)-0.06sin(5*2π0.2t)-0.03sin(7*2π0.2t)-0.2sin(9*2π0.2t)

Armónicos en la electricidad

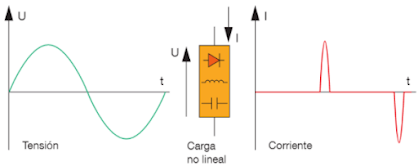
Cuando la corriente que atraviesa una carga tiene la misma forma que la tensión, esta cargase denomina lineal; por contra, cuando la forma de la corriente no se corresponde con la forma de la tensión, la carga se denomina no lineal.

Figura 5. Carga lineal

Figura 6. Carga no lineal

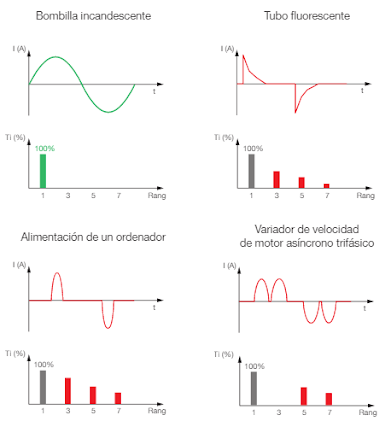
Un elemento esencial del estudio es el espectro de frecuencias armónicas de la señal; se trata de la representación gráfica que enumera los armónicos presentes, la señal en frecuencia y en amplitud. Aquí puede ver el espectro de algunas cargas habituales.

Figura 7. Cargas lineales y no lineales de algunos dispositivos eléctricos

Efectos generales de los armónicos sobre las redes eléctricas

Generados por los consumidores, los armónicos de corriente se propagan en las redes y crean distorsiones de la onda de tensión en las impedancias de las líneas. Estas deformaciones de la tensión se redistribuyen a los usuarios de todo el conjunto de la red del proveedor de energía eléctrica. El armónico de rango 3 merece especial atención en el caso de las redes trifásicas. En efecto, las corrientes de armónicos de rango 3 y sus múltiplos están en fase y se suman de forma vectorial en el conductor de neutro (In= I1 + I2 + I3). Si los receptores están formados principalmente por cargas informáticas, las corrientes de rango 3 y de rangos múltiplos de 3 se suman en el conductor neutro, lo que genera una corriente de neutro un 130% más elevada que las corrientes de fase.

Figura 8. En las corrientes trifásicas, las corrientes armónicas de rango 3 están en fase

Debe tenerse en cuenta que además de los armónicos indicados anteriormente, en las redes también se encuentran otros dos tipos de componentes superpuestos ala onda fundamental. Los inter-armónicos que se caracterizan por una frecuencia que no es múltiplo dela fundamental (por ejemplo: 175 Hz no es múltiplo de 50 Hz), y los infra-armónicos los cuales presentan una frecuencia inferior a la de la red.

Distorsión armónica total (THD)

La Distorsión Armónica Total (THD) es una medida de cuánto se «distorsiona» o cambia la forma de onda del voltaje o de la corriente de su forma senoidal convencional.

Medición de los armónicos presentes en una red

La resultante de los armónicos normalmente se explica por la distorsión armónica total (THD: Total Harmonics Distortion). El cálculo de THD permite calificar globalmente el nivel de contaminación de una red en tensión o en corriente.

Tabla 1

Interarmónicos en la electricidad

IEEE define los interarmónicos como “una componente en frecuencia de una señal periódica que no es un múltiplo entero de la frecuencia a la cual el sistema está operando”. IEC define los interarmónicos como “entre los armónicos de las señales de tensión y corriente, se pueden observar componentes de frecuencia que no son un múltiplo entero de la fundamental. Esas frecuencias pueden aparecer como frecuencias discretas o como un grupo amplio de frecuencias” . De forma sencilla, los interarmónicos son cualquier señal cuya frecuencia no es un múltiplo entero de la frecuencia fundamental. Existe un segundo grupo de interarmónicos cuya frecuencia es menor que la frecuencia fundamental. A este grupo se le conoce como “subarmónicos”.

Fuentes de interamonicos:

Cargas operando en estado transitorio:

Cargas con cambios rápidos en corriente y tensión son unas de las principales fuentes de interarmónicos. Los hornos de arco son un ejemplo de este tipo de cargas. Inicialmente, el horno de arco demanda una gran cantidad de corriente que va disminuyendo a medida que se derrite el metal que está siendo procesado.

Convertidores conmutados no sincronizados a la frecuencia fundamental:

Los sistemas de conmutación basados en tiristores están sincronizados con la frecuencia fundamental del sistema, por lo tanto, no producen interarmónicos. Por otra parte, las fuentes conmutadas basadas en IGBTs, que pueden ser conmutadas en cualquier momento, son una fuente de interarmónicos.

Cargas operando en saturación:

Por la construcción de su circuito magnético, los motores son una fuente de interarmónicos cuando estos están operando en la zona de saturación magnética. Cuando el motor tiene asimetrías en su construcción también produce frecuencias que no son múltiplo de la frecuencia fundamental [2], [4]. El torque variable también es una condición de operación que produce interarmónicos.

Consecuencias de los Interarmónicos:

Los efectos de los interarmónicos son similares a los efectos de los armónicos, como son las sobrecargas, distorsión en la forma de onda y posibles resonancias. Producen calentamiento adicional en los cables, lo cual contribuye a aumentar las pérdidas en el sistema. También interfieren en los sistemas de comunicación que usan el cable de la red para enviar los mensajes, por lo que se puede concluir que las comunicaciones son fuentes de interarmónicos y a la vez se ven afectados por los mismos. Tal vez el efecto más conocido de los interarmónicos es el parpadeo (o flicker en inglés), que es una variación de la iluminación que es perceptible al ojo humano

Figura 9. Tensión y espectro de frecuencia de un horno de arco

Continuando con el desarrollo de nuestros ejemplos, le hemos añadido un interarmonico de 0.5 Hz con amplitud de 0.2 y notamos que es lo que les ocurre:

Señal diente de sierra con un interarmonico

f(t)=2-1.27sin(2π0.2t)-0.64sin(2*2π0.2t)-0.42sin(3*2π0.2t)-…-0.13sin(10*2π0.2t)+0.2sin⁡(2π0.5t)

Interarmonico añadido: 0.2sin⁡(2π0.5t) -> en el espectro de frecuencia comprobaremos la magnitud y la frecuencia de esta.