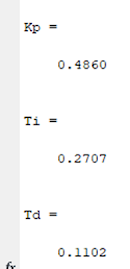Autores: Mauro Montoya Arenas
Leonel Alberto Breña
SINTONIZACION DE CONTROLADORES PID
Resumen: En el presente informe se analizó técnicas clásicas de sintonización de controladores PID como los son el método de Ziegler and Nichols y el controlador de por modelo interno. Además, se buscó la optimización de estos haciendo variaciones intuitivas con criterio para asegurar que los ajustes finos realizados son en pro de obtener una respuesta con parámetros aceptables. En la primera sección del informe se hizo uso del primer método de Z y N a un sistema aproximando a este a un modelo de primer orden con retardo y finalmente su buscó una optimización en la respuesta del sistema en lazo cerrado. En la segunda sección, se realizó la sintonización mediante IMC. Luego se varió la constante de tiempo para análisis de su efecto en el sistema. Finalmente, se realizó una simulación considerando perturbación en el sistema y se comparó la eficacia del método del IMC con el de ZyN.
I. INTRODUCCION
Los controladores PID tienen múltiples funciones y puede llevar a cabo el control de numerosos sistemas que van desde el control de una temperatura concreta hasta el de una dirección de un dispositivo móvil o, por ejemplo, el control de velocidad de un sistema automático. La primera ventaja del uso de reguladores PID es que con ellos podemos disminuir el tiempo de respuesta y hacer que esta sea mucho más rápida. Junto con la rapidez, también es posible configurar reguladores PID para conseguir de ellos una respuesta precisa, es decir que en determinadas ocasiones deberemos priorizar la precisión antes de la rapidez de respuesta del sistema.
Hay varias formas de sintonizar un controlador PID. Existen software diseñados para esto, como lo es el Simulink, los cuales estiman las dinámicas del proceso por la respuesta obtenida ante la variación de la referencia. Otros métodos están basados en la teoría de control, como por ejemplo el de Zieglers y Nichols. Estos métodos son una buena alternativa, pero en ocasiones requieren llevar al proceso a condiciones que en la práctica son perjudiciales o simplemente no son posibles, como hacer que el sistema se haga oscilatorio [2].
Otra técnica de un gran rendimiento es el controlador por modelo interno (IMC). El IMC ha sido mostrado como una estrategia de control con buenos resultados, gracias a su robustez, contra los efectos ocasionados por los disturbios y la inexactitud que presenta el modelo introducido con respecto al real [3].
II. MARCO TEORICO
Método de Ziegler y Nichols
Cuando pensamos en las ventajas de aplicar el método de sintonización propuesto por Ziegler y Nichols, la que posiblemente será más atractiva es que no hay necesidad de conocer la función de transferencia del sistema, ya que con conocer la respuesta de forma empírica y tener criterio para seleccionar una metodología adecuada para sintonización es suficiente para obtener un controlador con características aceptables en muchos casos.
- Primer método:
El primer método se basa en un análisis de la respuesta de forma experimental para luego realizar el proceso de sintonización. Si la planta no contiene integradores ni polos dominantes complejos conjugados, la curva de respuesta escalón unitario puede tener forma de S, como se observa en la Figura 1. Este método se puede aplicar si la respuesta muestra una curva con forma de S [1]. Los parámetros de interés se obtendrán trazando una recta tangente en el punto de inflexión de la respuesta del sistema como se ve a continuación.
Los parámetros por obtener son el tiempo de retardo (L) y la contante de tiempo T. Debemos tener en cuenta que en este primer método de ZyN aproximaremos el sistema a un sistema de primer orden con retardo.
Con los parámetros obtenidos, podemos realizar la sintonización dependiendo de qué tipo de controlador se adaptará mejor a nuestro sistema. Con frecuencia, un controlador PI es más que suficiente para nuestro sistema y el querer adicionar un término derivativo puede ser más perjudicial que benéfico para nuestro sistema.
El resultado de controlador PID mediante este primer método es el siguiente
Podemos concluir que el controlador tiene un polo en el origen y un cero doble en s=-1/L.
- Segundo método:
El segundo método consiste en básicamente variar el término proporcional K_p del controlador hasta llevar al sistema a su límite de estabilidad considerando T_i=∞ y T_d=0 y a partir de esto, realizar una sintonización. La respuesta del sistema al límite de su estabilidad será como la siguiente.
De la figura anterior obtendremos 2 parámetros: K_cr y P_cr los cuales representan la ganancia crítica y el periodo de oscilación respectivamente.
Para este método, Ziegler and Nichols propusieron los siguientes valores para el tipo de controlador que deseemos implementar.
Método del controlador por modelo interno (IMC)
La estructura de Modelo Interno de Control (IMC) propuesta inicialmente por los investigadores Morari y Zafiriou en los años 80, por lo que podemos decir que no es una metodología reciente.
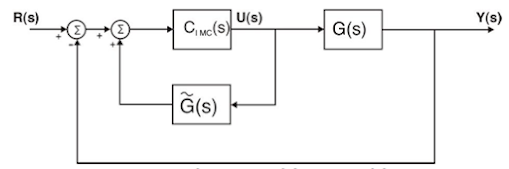
Está conformada por un controlador y un modelo del proceso real como veremos en la figura 3, en ocasiones llamado IM (Internal Model) representado por la zona punteada de la figura 3. La referencia [3] no dice que esta estructura de control se basa en el principio del IM donde el estado deseado de la variable controlada puede ser alcanzado si el sistema de control encapsula, ya sea implícita o explícitamente alguna representación del proceso a ser controlado.
Esto quiere decir que se implementará un modelo exacto del sistema real, un control perfecto sobre la variable controlada. La realimentación consistirá en la diferencia que hay entre la señal del modelo “perfecto” del IM y la salida del proceso real.
Si fuese un caso ideal podríamos hacer un control perfecto haciendo
Esto no es posible ya que G ̃(s) puede incluir una parte no invertible como ceros en fase no mínima y/o retardos puros.
Lo conveniente es dividir el modelo interno en una parte que se pueda invertir y otra que no de la siguiente manera
Adicionalmente, para atenuar errores de modelado se suele utilizar un filtro G_f (s) debido a diferencias entre el proceso y el modelo del proceso.
Este filtro será parte del controlador ayudando a que C_IMC sea propia, ya que irá en serie con el controlador. De forma práctica podemos hacer que n sea igual a 1 mientras que el valor de τ_f se tomará como la mitad de τ, para que el filtro sea más rápido que la dinámica del proceso.
El controlador finalmente sería de la siguiente manera
Aplicación del IMC para la sintonización para la sintonización de Controladores PID
Si nuestro proceso puede ser representado por un modelo de primer orden con retardo. Y a este retardo se le aplica la aproximación de Padé. Entonces, a partir de la estrategia de control IMC se podría hallar una sintonía para controladores PID. Veámoslo en el siguiente ejemplo:
Si el modelo del proceso viene dado como un modelo de primer orden con retardo, es decir:
Reemplazamos el término del retardo por su aproximación de Padé en la ecuación (12), obtenemos
Comparando las ecuaciones 11 y 12 obtenemos los parámetros K_P , T_i y T_d, los cuales se muestran en la siguiente tabla
III. MATERIALES Y METODOS
A. ESQUEMAS
B. PROCEDIMIENTO
1. En Matlab/Simulink halle la respuesta de nuestro proceso:
Este apartado se realizó haciendo uso de un script de Matlab donde mostramos solamente la respuesta del sistema ante una entrada tipo escalón unitario.
De la ecuación 16 sabemos que se trata de un sistema de tercer orden Observamos que la figura 10 nos muestra una respuesta sin sobre-impulsos, cosa que no fue ninguna sorpresa ya que los polos del sistema son los siguientes:
Ya que ubicamos los polos en el semiplano izquierdo y notando que no contiene parte imaginaria, el sistema no tendrá una respuesta con oscilaciones.
2. En Matlab/Simulink programe el lazo de control realimentado de la figura 1 considerando la ley de control del controlador PID según con la ecuación 1.
Codificando en Matlab podemos definir el controlador PID y hacerlo parte del sistema y crear la retroalimentación respectiva como se ve a continuación
Entonces, el sistema controlado queda definido con la siguiente instrucción:
HLC=feedback(G*Gs,1);
Donde Gs es la función de transferencia del sistema original de la ecuación 14 y G es el controlador PID. Haciendo la implementación en Simulink del controlador PID como en la figura 8 (ideal)
Almacenándolo en un subsistema y uniendo este controlador a la función de transferencia del sistema obtenemos lo siguiente
3. Sintonización del controlador PID
I. Método de Ziegler-Nichols
i. Con el modelo de primer orden con tiempo muerto de nuestro proceso, encuentre los parámetros del controlador PID usando el método de Ziegler-Nichols.
Primero, precisamos que, tras el análisis hecho en el primer apartado del procedimiento, observamos que el sistema no contiene oscilaciones en su respuesta y por ende, tampoco contiene sobre-impulso. Asemejándose así a un sistema de primer orden sobreamortiguado excepto por la concavidad que podemos ver al inicio de la respuesta transitoria. Dejando claro las observaciones anteriores, podemos decir que el sistema se puede aproximar a un sistema de primer orden con retardo que tendrá la forma mostrada en la ecuación 1.
Ahora, teniendo en cuenta el análisis hecho y las ecuaciones para el controlador PID de la tabla 1 y la ecuación 2, implementamos un script capaz de obtener los valores de 𝐾𝑃, 𝑇𝑖 y 𝑇𝑑.
De forma adicional a lo pedido, veremos la gráfica conjunta del sistema original, la entrada de excitación, el sistema de primer orden con retardo aproximado con la recta tangente que pasa por el punto de inflexión.
De esta forma se puede comprender de forma integral el procedimiento posterior de este método ya que podemos estimar de forma empírica los valores de las constantes que serán obtenidas posteriormente.
Del código de la figura 14 obtuvimos los valores de 𝐾𝑃, 𝑇𝑖 y 𝑇𝑑.
Corroborando de forma analítica, partimos de los valores de T y L obtenidos del modelo de primer orden
T=0.2457 L=0.05 (18)
De estos valores en las equivalencias de la tabla 1 para un controlador PID
Comprobamos la correcta obtención tanto de forma manual y con herramientas computacionales.
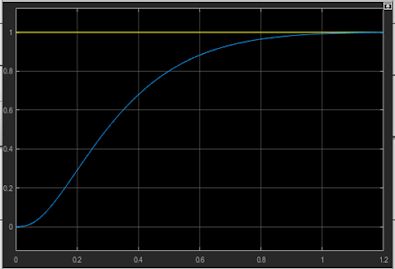
ii. Realice una simulación del comportamiento del sistema de control ante un cambio en la consigna (escalón unitario) usando la sintonía obtenida.
Ahora, haremos un cambio en el valor del escalón para ver la efectividad de nuestro controlador. El cambio de consigna será ahora un step de magnitud 5 como se ve en la siguiente gráfica
Vemos que el controlador cumple su rol fundamental de llevar al sistema al valor de la consigna en estado estacionario. Ahora, haciendo la implementación en Simulink tenemos lo siguiente:
Veamos que se ingresaron los valores como variables que ya han sido declaradas en el workspace, como evidencia de ello estarán disponibles los archivos de simulación en el archivo comprimido.
A continuación, mostramos los resultados de simulación
Ahora realizando el cambio en la consigna
iii. Grafique la salida del sistema junto con la consigna del sistema.
Graficando tanto la consigna como la salida vemos que el controlador cumple la función obligatoria aparte de estabilizar el sistema la cual es llevar la respuesta al valor de la referencia.
Observación: Hay una diferencia en las respuestas obtenidas en Matlab y Simulink en la magnitud en el estado estacionario. Atribuimos esta diferencia al filtro que está implícito en el bloque diferencial de Simulink.
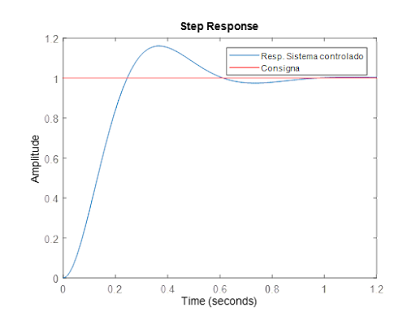
iv. De obtener un sobre impulso mayor al 25%. Realice un ajuste fino de los parámetros.
Para que el impulso sea menor al 25%, el valor máximo debería estar por debajo de 1.25, por lo tanto, vemos en la figura que sobrepasa este valor de forma significativa.
El ajuste fino que realizamos está en el término proporcional
Podemos ver que haciendo ajustando el término proporcional podemos obtener respuestas con menor overshoot pero su vez, vemos que también varía el tiempo de estabilización. Podemos seguir ajustando hasta obtener valores como se ve a continuación.
Vemos en la figura 32 que con K_p/20 obtenemos una respuesta con mayor retardo y sin sobre impulso. Dependiendo del sistema físico y de los requerimientos deseados para un rendimiento óptimo. Escogeremos la respuesta que más se ajuste de acuerdo a las necesidades de la planta.
II. Método de IMC
i. Con el modelo de primer orden con tiempo muerto de nuestro proceso, encuentre los parámetros del controlador PID usando el método del IMC, considerando τ_f=𝝉/2.
KP =_____, Ti=_____y Td=_____
Modelo de primer orden del sistema:
Para hallar las constantes tau, tm y k debemos seguir el procedimiento de Ziegler and Nichols, definimos la variable “y” como la respuesta al escalón en el tiempo. Después derivamos “y” y obtenemos la pendiente “m” y el punto “p” donde ocurre la inflexión (máximo valor de la derivada).
Obtenemos a continuación el tiempo y la magnitud en el punto de inflexión. El tiempo de retardo “tm” será igual al tiempo en el cual la curva llega al punto de inflexión menos la altura del punto de inflexión dividido entre la pendiente. El “tau” es igual al valor estacionario de la respuesta menos el punto de inflexión entre la pendiente, todo sumado al tiempo en la inflexión menos el tiempo muerto. La constante “k” será el valor estacionario de la respuesta entre el tiempo estacionario de la entrada.
A partir de aquí podemos hallar las constantes kp, Ti y Td, necesarias para el controlador
Figura 35. Hallamos las constantes
Kp=0.1831, Ti=0.2707, Td=0.0415
ii. Realice una simulación del comportamiento del sistema de control ante un cambio en la consigna (escalón unitario) usando la sintonía obtenida.
Utilizaremos el siguiente modelo:
Donde:
En Matlab:
En Matlab primero, según el enunciado, definimos la constante t_f=τ/2, y calculamos los parámetros Kp, Ti y Td según la tabla 4.
En simulink:
En simulink, hemos obtenido los parámetros Kp, Ti y Td del script creado en Matlab. Después construimos el diagrama de bloques según el modelo PID.
iii. Grafique la salida del sistema junto con la consigna del sistema.
En Matlab:
En simulink:
iv. Repita la simulación considerando τ_f=𝝉/8 y τ_f=2𝝉. ¿Cuál es el efecto en la respuesta del sistema?
Para t_f=τ/8
En Matlab:
En Matlab primero, según el enunciado, definimos la constante t_f=τ/8, y calculamos los parámetros Kp, Ti y Td según la tabla 4.
Kp=0.4860, Ti=0.2707, Td=0.1102
En simulink:
En simulink, hemos colocado los parámetros Kp, Ti y Td que obtuvimos del script creado en Matlab (podemos verificar que son los mismos valores que aparecen en la figura 43).
Observación:
Hemos considerado un sistema con controlador PID en el que el termino derivativo sea “s” puro, sin embargo, en el caso que lo consideremos la parte derivativa como un filtro: s/(sN+1), la salida seria la siguiente:
Efecto de la respuesta en el sistema:
Podemos observar que el efecto de que t_f=τ/8 provoca una sobreelongacion (un pico máximo y minimo), con la función “Cursor Measurements” podemos medir el tiempo en el que ocurre la sobreelongacion y la magnitud de este:
La sobreelongacion ocurre en el tiempo 0.069 y su magnitud es de 1.081, y el pico mínimo ocurre en el tiempo 0.132 y su valor es de 0.132.
Para t_f=2τ
En Matlab:
En Matlab primero, según el enunciado, definimos la constante t_f=2τ, y calculamos los parámetros Kp, Ti y Td según la tabla 4.
Kp=0.0524, Ti=0.2707, Td=0.0119
En simulink:
En simulink, hemos colocado los parámetros Kp, Ti y Td que obtuvimos del script creado en Matlab (podemos verificar que son los mismos valores que aparecen en la figura 50).
Efecto de la respuesta en el sistema:
Podemos observar que el efecto de que t_f=2τ provoca que el sistema sea sobreamortiguado. Ya no tiene sobreelongaciones pero se demora más en llegar a la referencia.
4. Compare estas dos respuestas ¿Cuál tiene un mejor desempeño? Justifique su respuesta basado en algún criterio integral.
Comparación de las respuestas del IMC (cuando t_f=τ/2, cuando t_f=τ/8 y t_f=2τ) y del método Ziegler and Nichols a través de los criterios integrales de error absoluto (IAE) e integral del tiempo por el error absoluto (ITAE)
En Matlab
Ziegler and Nichols
Recordemos que como la entrada es escalón unitario, la función en el tiempo de esta lo tomaremos como 1. Por lo tanto, el error es e(t)=1-y(t). Siendo y(t) la función de salida en el dominio del tiempo. Para calcular la integral usaremos la función “trapz”, que sirve para calcular una integral a través del método numérico conocido como trapezoide:
Para el método de Ziegler and Nichols: IAE=0.1345, ITAE=0.0260
IMC
Para el caso de t_f=τ/2:
Recordemos que como la entrada es escalón unitario, la función en el tiempo de esta lo tomaremos como 1. Por lo tanto, el error es e(t)=1-y1(t). Siendo y1(t) la función de salida en el dominio del tiempo. Para calcular la integral usaremos la función “trapz”, que sirve para calcular una integral a través del método numérico conocido como trapezoide:
Para t_f=τ/2: IAE=0.1478, ITAE=0.0323
Para el caso de t_f=τ/8:
Recordemos que como la entrada es escalón unitario, la función lo tomaremos como 1. Por lo tanto, el error es e(t)=1-y2(t). Siendo y2(t) la función de salida en el dominio del tiempo. Para calcular la integral usaremos la función “trapz”, que sirve para calcular una integral a través del método numérico conocido como trapezoide:
Para t_f=τ/8: IAE=0.0601, ITAE=0.0091
Para el caso de t_f=2τ:
Recordemos que como la entrada es escalón unitario, la función lo tomaremos como 1. Por lo tanto, el error es e(t)=1-y3(t). Siendo y3(t) la función de salida en el dominio del tiempo. Para calcular la integral usaremos la función “trapz”, que sirve para calcular una integral a través del método numérico conocido como trapezoide:
Para t_f=2τ: IAE=0.5161, ITAE=0.3021
En simulink
Para hacerlo en simulink debemos ahora transladar los valores de simulink a Matlab con el bloque “To workspace” para realizar el IAE y el ITAE.
Ziegler and Nichols
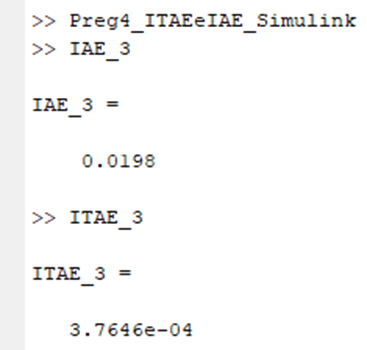
Para el método de Ziegler and Nichols: IAE= 0.0198, ITAE=0.0003764
IMC
Para el caso de t_f=τ/2:
Para t_f=τ/2: IAE=0.0179, ITAE=0.0002604
Para el caso de t_f=τ/8:
Para t_f=τ/8: IAE=0.0195, ITAE=0.00046135
Para el caso de t_f=2τ:
Figura 71. Sistema con Controlador PID-IMC con t_f=2τPara t_f=2τ: IAE=0.0546, ITAE=0.0031
Observación: Hemos visto que la medición del IAE y del ITAE son distintos en Matlab y Simulink. Esto es debido a distintos factores: Primero, los puntos de análisis que se toman en Matlab y Simulink. Ademas, en simulink se considera un filtro (s/s+1) en lugar de una derivada “s”. Además, es imposible integrar desde 0 hasta infinito, en Matlab integramos de 0 a 5 (la simulación se ralentiza si tomamos más puntos), y en simulink integramos de 0 a 10. Eso hace que las mediciones sean distintas. Tomaremos de referencia el simulink
¿Cual tiene mejor desempeño?
Analizando los resultados obtenidos de tiempo de error absoluto y del tiempo por el error absoluto, podemos decir que cuando t_f=τ/2 el sistema presenta mejor desempeño. Ya que los valores del IAE y del ITAE son menores. Seguido del método con controlador IMC con t_f=τ/8. Aunque hay que recalcar que el sistema cuando t_f=τ/8, presenta sobreelongaciones que podrían dañar el sistema. Podemos darnos cuenta que el siguiente que sigue en la lista de desempeño es el método Ziegler and Nichols. El que tiene peor desempeño es el IMC con t_f=2τ. A continuación, mostramos una gráfica del scope con todas las respuestas del sistema.
Señal amarilla: Control PID-Z&N
Señal rojo: Control PID-IMC con t_f=τ/8
Señal celeste: Control PID-IMC con t_f=τ/2
Señal verde: Control PID-IMC con t_f=2τ
5. Ahora en el lazo de control realimentado programado en el ejercicio 2, agregue una entrada de perturbación en la entrada del proceso.
Hemos introducido una distorsión tal y como indica el enunciado. Analizaremos la salida utilizando ambos métodos.
Ziegler and Nichols:
IMC:
6. Simule el sistema con una perturbación escalón de magnitud del 2% de la entrada tanto para la sintonía obtenida por el método Ziegler-Nichols como para la obtenida usando IMC.
Ziegler-Nichols:
Análisis: Para el caso del control PID-Z&N, introducirle una distorsión no provoco demasiada alteración en cuanto al comportamiento de la respuesta.
IMC:
Análisis: Para el caso del control PID-IMC, introducirle una distorsión hizo que la señal de salida alcanzara un valor más cercano al valor de la referencia.
7. Compare estas dos respuestas ¿Cuál tiene un mejor desempeño? Justifique su respuesta basado en algún criterio integral.
Comparación:
Para realizar la comparación extraigo los valores de salida de ambos sistemas (usando el bloque To workspace) y calculo la integral del error absoluto (IAE) y la integral del tiempo por el error absoluto (ITAE):
Z&N:
Para Z&N: IAE=0.2363, ITAE=0.0421
IMC:
Para t_f=τ/2: IAE=0.2229 e ITAE=0.0319
¿Cual tiene mejor desempeño?
Analizando los resultados obtenidos de tiempo de error absoluto y del tiempo por el error absoluto. Podemos decir que el PID–IMC tiene mejor desempeño que el PID- Z&N con t_f=τ/2 cuando se le introduce una perturbación. Ya que el PID–IMC t_f=τ/2 no le afecta tanto el ruido como al PID- Z&N.
8. Investigue sobre alguna regla de sintonía para controladores PID basado en los criterios de desempeño de los sistemas de control (IAE, ISE, ITAE).
El método basado en criterios integrales que se presenta es el Método de López, Miller, Smith y Murril, más conocido como el método López ya que este fue el primero en postularlo. Este método presentó ecuaciones para el cálculo de los parámetros del controlador. Definiendo una función de costo de la forma:
Donde F es una función del error y del tiempo, se obtiene un valor que caracteriza la respuesta del sistema. Entre menor sea el valor de Φ, mejor será el desempeño del sistema de control, por ello, un desempeño óptimo se obtiene cuando Φ es mínimo. Como Φ es una función de los parámetros del controlador (Kc, Ti, Td), el valor mínimo de Φ se obtiene resolviendo las siguientes ecuaciones
Los criterios de desempeño utilizados por López fueron: Integral del error absoluto (IAE), Integral del error absoluto por el tiempo (ITAE) e Integral del error cuadrático (ISE). La optimización de los criterios de desempeño integrales de López está basada en el mejor modelo de primer orden más tiempo muerto que se pueda obtener, para lazos de control que funcionan como reguladores con un controlador PID-Ideal. Las ecuaciones de sintonización son:
Los valores para las constantes ‘a’ hasta ‘f’ para los diferentes criterios se encuentran en la tabla siguiente.
Siendo el controlador:
9. Sintonice un controlador PID para el proceso G(s) basado en la regla investigada en el punto anterior.
ITAE (método de López)
a=1.357, b=-0.947, c=0.842, d=-0.738, e=0.381, f=0.995
Con los parámetros obtenidos de Ziegler and Nichols:
k=0.5901, tm=0.05, Tau=0.2457
Nos toca hallar K_c,T_d y T_i
Ahora armamos nuestro diagrama de bloques en Simulink y analizamos la respuesta:
Figura 89. Diagrama de bloques del PID con el método de LópezAnálisis:
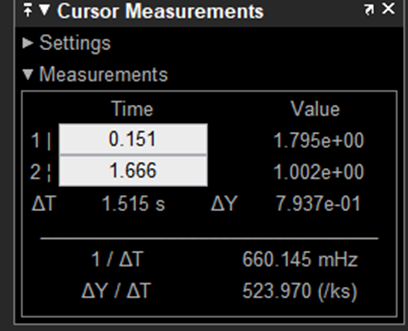
Podemos observar que con este método se le da más énfasis a la constante. Podría ser útil para aproximarnos de forma más rápida a la salida sin importar que el sistema sea oscilatorio. Sin embargo, la sobreelongacion que tiene puede ser muy perjudicial. En a siguiente figura analizamos dicha sobreelongacion:
Observamos que para el tiempo 0.159 segundos el sistema tiene una altura máxima de 1.795. Y se estabiliza en el tiempo 1.666 segundos
10. Compárela con las sintonías anteriores.
Comparación de la sintonía para controladores PID basado en el método de López y sintonía por IMC y Ziegler and Nichols
Observando las gráficas de respuestas podemos hacer las siguientes comparaciones:
- El controlador PID con el método de López tiene mayor sobreelongacion y presenta mayor oscilación. Aunque llega al valor de referencia más rápido y se estabiliza aproximadamente a los 1 segundos.
- El controlador PID-Z&N es el que más se parece al controlador PID con el método de López. Ambos presentan sobreelongaciones y oscilaciones. Aunque el controlador PID-Z&N no tiene cambios tan abruptos.
- El controlador PID con el método de López prioriza llegar más rápido a la referencia. Está diseñado para hacer que el error sea de “0” lo más rápido posible. Aunque eso implique tener un comportamiento brusco, que puede ocasionar en pérdidas de energía y altos voltajes en la salida.
IV. CONCLUSIONES
El controlador PID-IMC con t_f=τ/2 y t_f=2τ la respuesta presenta una respuesta al escalón de tipo sobreamortiguado. Mientras que un controlador PID-IMC con t_f=τ/8, presenta una respuesta al escalón de tipo subamortiguado.
Una de las características que debemos tener en cuenta es el rechazo a las perturbaciones. Hemos comprobado en la guía, a través de los criterios integrales de IAE e ITAE que el controlador PID-Z&N presenta un mayor rechazo de perturbaciones que el controlador PID-IMC con t_f=τ/2.
Las sobreelongaciones generan más esfuerzo de control. Cuando un sistema tiene un comportamiento oscilatorio va a generar cambios bruscos dependiendo de cuan oscilatorio sea el sistema. Esto, en algunos casos no genera mayores problemas. Pero en otros casos va a hacer evitable y es preferible elegir un controlador PID que no presente este movimiento oscilatorio y que no sobrepase el valor de la referencia.
El controlador PID-Método de López llega muy rápido al valor de referencia, pero es el que tiene un mayor pico en su respuesta de salida (casi un 80% mayor que su voltaje de referencia).
Se concluye que un controlador PID nos brindará un sistema que efectivamente cumpla con llegar al nivel de referencia a distintos cambios en la consigna del sistema.
Se puede realizar ajustes en el controlador PID dependiendo de los requerimientos del proceso o para cuidar el sistema de daños ante los picos en la etapa transitoria. Asimismo, podemos variar la velocidad de respuesta.
V. REFERENCIAS
[1] Katsuhiko Ogata. Teoría de Control Moderna. Cap. 7.
[2] https://controlreal.com/es/pid-como-sintonizar-un-lazo-pid/#:~:text=El%20algoritmo%20funciona%20adecuadamente%20cuando,y%20se%20mide%20la%20respuesta.
[3] García Yhon y Lobo Israel. Controlador PID por la estructura de control de modelo interno (IMC) y lógica difusa.