Autores: Mauro Montoya Arenas

Leonel Alberto Breña

REPASO DE MATLAB - SIMULINK

Resumen: En este laboratorio hacemos un repaso de las funciones básicas que podemos hacer con Matlab y Simulink. Empezamos primero con una breve explicación de estos 2 softwares: en que areas de la ingenieria se usa y cuáles son sus ventajas. Profundizamos más la explicación de su uso en el area de sistemas de control, también describimos la interfaz del software de Matlab (command window, workspace, entre otros). Seguidamente, hallamos el lugar geométrico de las raices de un sistema. Después dividimos un sistema en funciones parciales. Hallamos la respuesta de un sistema con las 3 entradas más comunes: impulso, escalón y rampa (en Matlab y Simulink). Para finalizar hemos preparado unas conclusiones producto de la realización del laboratorio.

I. INTRODUCCION

En las diversas áreas de trabajo e investigación, el manejo de software es de suma importancia, y más aún lo es la habilidad del manejo de este acompañado de una sólida base teórica. Enfocándonos en los sistemas de control, el software Matlab nos ofrece un entorno para realizar programas que modelen sistemas de interés, para ello, debemos tener información detallada del comportamiento físico del sistema.

Además de ellos contamos con la herramienta Simulink, con la cual podremos expresar nuestros sistemas y visualizar las respuestas temporales de estos. La presente experiencia de laboratorio busca consolidar las destrezas que tenemos en el manejo del software Matlab y, más aún en la justificación teórica que, como estudiantes de ingeniería, debemos dominar de forma integral.

Entonces, una vez representado un sistema, seremos capaces de evaluar, en el dominio temporal, dichos sistemas ante diversos tipos de entrada como el escalón, rampa e impulso unitario y a su vez, corroborar resultados, ya que recurrimos tanto a la herramienta de digitación de código de programación y a la herramienta Simulink.

II. MARCO TEORICO

MATLAB

MATLAB es el nombre abreviado de “MATriz LABoratory”. Es un programa para realizar cálculos numéricos con vectores y matrices, y por tanto se puede trabajar también con números escalares (tanto reales como complejos), con cadenas de caracteres y con otras estructuras de información más complejas.

Matlab es un lenguaje de alto rendimiento para cálculos técnicos, es al mismo tiempo un entorno y un lenguaje de programación. Uno de sus puntos fuertes es que permite construir nuestras propias herramientas reutilizables. Podemos crear fácilmente nuestras propias funciones y programas especiales (conocidos como M-archivos) en código Matlab, los podemos agrupar en Toolbox (también llamadas librerías): colección especializada de M-archivos para trabajar en clases particulares de problemas [1].

Matlab es usado en distintos ámbitos de la ingeniería como, por ejemplo:

-Análisis de datos: MATLAB facilita tareas de data science con herramientas para acceder y preprocesar datos, crear modelos predictivos y de machine learning, y desplegar modelos en sistemas de IT empresariales [2].

Figura 1. Machine learning aplicado en MATLAB

-Comunicaciones inalámbricas: MATLAB genera formas de onda personalizables para verificar la conformidad con los últimos estándares de 5G, LTE y WLAN, crea modelos con elementos de tipo digital, RF y antena para explorar y optimizar el comportamiento del sistema, genera automáticamente código HDL o C para el prototipado y la implementación sin tener que generarlo de forma manual, entre otras cosas [3].

-Procesamiento digital de señales: Los ingenieros de procesamiento de señales utilizan MATLAB y Simulink en todas las etapas del desarrollo, desde el análisis de las señales y la exploración de los algoritmos hasta la evaluación de los tradeoffs en la implementación de los diseños para la creación de sistemas de procesamiento de señales en tiempo real [4].

Figura 2. Diseño de filtros en MATLAB

-Robótica: Con MATLAB y Simulink se puede conectar con su robot y controlarlo con los algoritmos que desarrolle. Desarrollar algoritmos independientes del hardware y conectar con Robot Operating System (ROS). Conectar con una serie de sensores y actuadores para poder enviar señales de control o analizar diversos tipos de datos. Eliminar la creación manual de código gracias a su generación automática para plataformas embebidas tales como microcontroladores, FPGAs, PLCs y GPUs en diversos lenguajes, como C/C++, VHDL/Verilog, texto estructurado (ST) y CUDA, entre otras cosas [5].

Figura 3. Robot ajedrecista con toma de decisiones programado en Matlab

-Sistemas de control: Los ingenieros de sistemas de control utilizan MATLAB y Simulink en todas las etapas de desarrollo, desde la modelización de la planta hasta el diseño y ajuste de los algoritmos de control y la lógica de supervisión, finalizando con la implementación gracias a la generación automática de código y la verificación, validación y comprobación del sistema. MATLAB y Simulink ofrecen [6]:

· Un entorno de diagramas de bloques multidominio para modelizar la dinámica de la planta, diseñar algoritmos de control y ejecutar simulaciones de lazo cerrado.

· Modelización de plantas mediante herramientas de modelización física o identificación del sistema.

· Funciones prediseñadas y herramientas interactivas para analizar el sobreimpulso, el tiempo de subida, el margen de fase, el margen de ganancia y otras características de rendimiento y estabilidad en los dominios de la frecuencia y el tiempo.

Figura 4. Diseño y ajuste de compensadores de retroalimentación

· Lugar de raíces, diagramas de Bode, LQR, LQG, control robusto, control predictivo de modelos y otras técnicas de diseño y análisis.

· Ajuste automático de sistemas de control PID, de ganancia programada y SISO/MIMO arbitrarios.

· Modelización, diseño y simulación de la lógica de supervisión para llevar a cabo la planificación, el cambio de modo y la detección, aislamiento y recuperación de errores (FDIR).

Figura 5. GUI que muestra una gráfica en 3D hecha en Matlab

Características básicas del Matlab

Nada más abrir Matlab (podemos hacerlo pinchando en el icono que aparece en el escritorio o en su defecto en Inicio->Todos los programas) aparecerá una pantalla como la siguiente:

Figura 6. Ventana de Matlab

Todas las sentencias que vamos a utilizar las escribiremos en la ventana Command Window (ventana de comandos). Es la ventana de mayor tamaño.

Si queremos información acerca de las variables que estamos utilizando en Matlab podemos verlas en la ventana Workspace (espacio de trabajo) o usar: who para obtener la lista de las variables (no de sus valores) whos para obtener la lista de las variables e información del tamaño, tipo y atributos (tampoco da valores) Para ver esta ventana tenemos que pinchar en la pestaña que tienen este nombre. Está en la parte superior izquierda:

Figura 7. Workspace del Matlab

Si lo que queremos es conocer el valor que tiene una variable lo hacemos escribiendo el nombre de la variable y pulsando Intro. Para recordar órdenes previas usamos las flechas del teclado ↑ y ↓. También podemos verlas en la ventana Command History, ventana situada en la parte inferior izquierda:

Figura 8. Command History del Matlab

SIMULINK

Una herramienta poderosa dentro del software Matlab es el muy conocido Simulink, cuyas aplicaciones son muy diversas, como podemos mencionar que, durante este curso, lo utilizamos para el modelamiento de sistemas de control de una complejidad no muy elevada, este modelamiento puede tener aplicaciones como en sistemas de procesamiento de señales, IOT, etc.

Simulink pueden ayudarle a diseñar, prototipar y desplegar aplicaciones IoT tales como mantenimiento predictivo, optimización de operaciones, control de supervisión, etc [8].

Figura 9. Sistema IOT en Simulink.

El espacio de trabajo de Simulink

Con motivo de aspirar a un entendimiento integral del presente informe, se muestran características básicas respecto entorno de trabajo de Simulink. En el espacio de trabajo de Simulink crearemos un modelo insertando los bloques correspondientes.

En primer lugar, hemos de insertar bloques de tipo Función de Transferencia en el modelo. Para ello tecleamos la palabra transfer en el campo de búsquedas o identificamos el bloque en library browser

Figura 10. Identificando el bloque Transfer Fcn.

En la ventana que se abre en cada caso, introduciremos los vectores de coeficientes de los polinomios numerador y denominador de cada función de transferencia.

Figura 11. Ventana para ingresar coeficientes de la F.T.

De esta manera, solo resta unir los bloques ya definidos y asignar una entrada deseada. El resultado final podría ser uno de los sistemas que se usaron en la experiencia.

Figura 12. Ejemplo de sistema de control implementado en Simulink.

Siguiendo esta línea e integrando más conocimientos en Simulink, se pueden llegar a crear aplicaciones más complejas como el control de un drone y su simulación en simulación en Simulink [9]

Figura 13. Ejemplo de aplicación de controlador en Simulink

III. MATERIALES Y METODOS

A. EQUIPOS, MATERIALES Y HERRAMIENTAS UTILIZADAS

Figura 14. Software Matlab

Figura 15. Software Simulink

B. ESQUEMAS

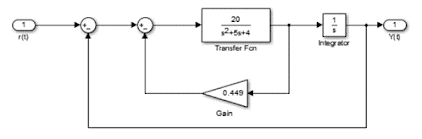
Figura 16. Sistema 1

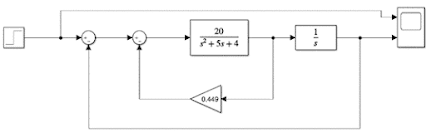
Figura 17. Sistema 2

C. PROCEDIMIENTO

a. Parte 1: Matlab

i. Obtener la representación gráfica en el plano s de los polos y ceros de G1(s).

Hallaremos la representación gráfica en el plano s de los polos y ceros de G₁(s) utilizando la función “pzmap”:

Figura 18. Script para hallar los polos y ceros de G₁(s)

Cuando lo grafiquemos tenemos la opción de cambiar el color y el tamaño de los polos y ceros en la gráfica dándole clic a la flecha de la parte superior, después a “Color” (para cambiarle a color) y a “Line Width” (para cambiar el tamaño).

Figura 19. Con “Color” y “Line Width” cambiamos el color y tamaño de los polos y ceros respectivamente

Escogimos el color rojo y el tamaño de la línea=4.0

Figura 20. Polos (“x”) y ceros (“o”) de G₁(s)

Podemos conocer el valor de cada polo y cero si le damos clic a este.

Figura 21. Información de los polos y ceros del sistema G₁(s)

De la gráfica podemos observar:

ii. Presentar el equivalente en funciones parciales de G2(s)

Antes de mostrar vamos a expresar dicha funcion en polos y ceros con la funcion “zpk”:

Figura 22. G₂(s) expresado en de forma factorizada

Podemos ver que G₂(s) tiene 3 polos en z=2. Ahora utilizo la función “residue” para hallar los numeradores, denominadores y residuos. Debemos saber además que para obtener las funciones parciales: los denominadores serán: (z+1), (z-2), (z-2)² y (z-2)³.

Figura 23. Programación para obtener las funciones parciales de G₂(s)

Figura 24. Funciones parciales de G₂(s)

iii. Halle la respuesta de G3(s), ante entradas escalón, impulso y rampa unitaria

Recordemos que para hallar la respuesta del sistema G₃(s) ante una entrada escalón usamos la función “step”, para una entrada impulso usamos “impulse” y ante una entrada rampa no existe una función definida, pero podemos usar la función “lsim”. Con esta función introducimos primero el sistema G₃(s), después la función de entrada (para la rampa será “t”) y el tiempo (t=0:0.01:6).

Antes de pasar a la programación de las respuestas ante dichas entradas. Observamos si G₃(s) es estable:

Figura 25. Analizamos la estabilidad de G₃(s)

Figura 26. Lugar geométrico de los polos y ceros de G₃(s)

Observando la figura 26, nos podemos dar cuenta que el sistema G₃(s) es estable. Además, como tiene sus raíces complejas y conjugadas, el sistema es subamortiguado. Pasamos ahora a introducirle entradas impulso, escalón y rampa, para observar sus respuestas.

Figura 27. Programación de la función impulso, escalón y rampa

Figura 28. Respuesta del sistema G₃(s) a la función impulso

Figura 29. Respuesta del sistema G₃(s) a la función escalón

Figura 30. Respuesta del sistema G₃(s) a la función rampa

Análisis de resultados: Podemos ver en el ejercicio “i” de la parte a, el lugar geométrico de los polos y ceros. Recordemos que para que un sistema sea estable, sus polos deben estar en la zona negativa. En el ejercicio “ii” hallamos G₂(s) expresado en funciones parciales usando el comando “residue” que devuelve: los numeradores, denominadores y residuo. En el ejercicio “iii” encontramos la respuesta respuesta de G₃(s) ante las entradas escalón, impulso y rampa. Viendo las gráficas podemos darnos cuenta que G₃(s) es estable, ya que la respuesta se estabiliza en el infinito para las entradas acotadas (impulso y escalón).

iv. Halle la respuesta ante el escalón, rampa e impulso de los siguientes sistemas. (Utilice solo comando de Matlab).

Definiendo entradas y salidas de cada sistema 1.

Figura 30. Sistema 1 con entradas y salidas definidas

Figura 31. Script de simulación

Figura 32. Respuesta ante entrada escalón

Figura 33. Respuesta ante una entrada impulso

Figura 34. Respuesta ante una entrada rampa

Definiendo entradas y salidas de cada sistema 2.

Figura 35. Sistema 2 con entradas y salidas definidas

Figura 36. Script para simulación

Figura 37. Respuesta ante una entrada escalón

Figura 38. Respuesta ante entrada impulso

Figura 39. Respuesta ante entrada rampa

Análisis de resultados: Para realizar este apartado, usamos una técnica en la cual, definimos las entradas y salidas del cada subsistema, además definimos cada punto de suma para finalmente hacer la síntesis del sistema como tal, usando el comando “connect”. A partir de ello, generamos las respuestas temporales para las diferentes entradas requeridas por la experiencia. Resaltamos que para la respuesta ante una rampa es necesario usar el comando “lsim” la cual nos permite la evaluación del sistema ante entradas arbitrarias, ya que la función rampa no cuenta con un comando específico.

b. Parte 2: Simulink

i. En simulink visualice la respuesta de los sistemas 1 y 2, ante las entradas, escalón, rampa e impulso.

Se muestra el sistema 1 evaluado a entradas escalón (figuras 40 y 41), rampa (figuras 42 y 43) e impulso unitario (figuras 44 y 45) con sus respectivas respuestas temporales.

Figura 40. Sistema 1 ante una entrada tipo escalón

Figura 41. Respuesta ante entrada escalón

Figura 42. Sistema 1 ante entrada rampa

Figura 43. Respuesta ante entrada rampa

Figura 44. Sistema1 ante entrada impulso (bloque derivativo en la salida)

Figura 45. Respuesta ante entrada impulso

A continuación, se muestra el sistema 2 evaluado a entradas escalón (figuras 46 y 47), rampa (figuras 48 y 49) e impulso unitario (figuras 50 y 51) con sus respectivas respuestas temporales.

Figura 46. Sistema2 ante una entrada tipo escalón

Figura 47. Respuesta ante entrada escalón

Figura 48. Sistema2 ante una entrada tipo rampa

Figura 49. Respuesta ante entrada tipo rampa

Figura 50. Sistema2 ante una entrada tipo impulso

Figura 51. Respuesta ante entrada tipo impulso

Análisis de resultados: En este apartado implementamos los sistemas de las figuras 30 y 35 para asegurar la efectividad de nuestra técnica y resultados adquiridos en el apartado iv. En Simulink, no contamos con un bloque que represente una entrada tipo impulso que funcione con un sistema en tiempo continuo como los que tenemos, así que, para lograr la respuesta deseada, utilizamos un boque derivativo a la salida del sistema, pues sabemos que la derivada de una función escalón es efectivamente un impulso unitario. Finalmente, ajustamos el tiempo de simulación para que coincida con los adquiridos en el apartado anterior y, en efecto, las respuestas son congruentes.

IV. CONCLUSIONES

· Observando la representación gráfica de los polos y ceros podemos darnos cuenta de la naturaleza del sistema. Un sistema cuyos polos se encuentren en la parte real positiva será inestable. Si se encuentra en el eje imaginario es críticamente estable. Y si se encuentra en la parte real negativa puede ser subamortiguado (raíces complejas), sobreamortiguado (raíces reales) o críticamente amortiguado (raíces iguales y reales).

· Todo sistema que tenga un numero de orden mayor o igual de 2 se puede separar en fracciones parciales. Cada fracción parcial puede significar un sistema más pequeño. Y la suma de estas funciones parciales significa que todas estas están en paralelo.

· Se puede comprobar la estabilidad de un sistema observando la respuesta de este ante una entrada acotada. Si el sistema es estable la salida también debe ser acotada.

· A partir de la mayor oscilación de la respuesta del sistema 2 en las figuras 19, 20 y 21, podemos asegurar que la distribución de sus polos tiende al eje imaginario en mayor medida que el sistema 1 de la figura 30.

· Las respuestas temporarias tanto en el código del apartado a. parte iv, son absolutamente congruentes con las obtenidas en el apartado b. gracias al buen manejo del software y de nociones teóricas como la representación de una entrada impulso ayudándonos del bloque derivativo.