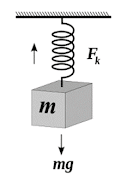
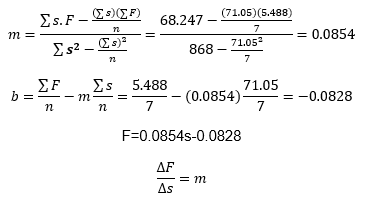CONSTANTES ELASTICAS (EXPERIENCIA Nº1)
OBJETIVOS:
- Determinar la constante elástica del material a trabajar
- Comprobar la relación directa entre el estiramiento del resorte y la fuerza elástica formada.
MONTAJE 1
Monte el equipo, como muestra el diseño experimental.
1. Utilice la balanza para determine los valores de las masas del resorte y del porta pesas.
¿Cree Ud. que le servirá de algo estos valores?
¿Por qué?
Tienen importancia ya que al momento de iniciar el experimento los datos a medir, como es la Fuerza, influirán ya sea si utilizamos solo la masa del resorte o consideramos la masa del portapesas lo cual será mas fuerza.
2. Cuelgue al resorte de la varilla y anote la posición de su extremo inferior.
Posición 1: 70.5 cm
3. Luego, coloque la porta pesas en el extremo inferior del resorte y anote la posición correspondiente.
Posición 2: 70.4 cm
4. Seguidamente, coloque una pesa pequeña [m= 0.050 kg] en la porta pesas y anote la posición correspondiente.
Posición 3: 69.8 cm
5. Adicione pesas a la porta pesas, cada vez de mayores masas. En la Tabla 1 anote los valores de las posiciones correspondientes (incluida la posición de referencia).
6. Ahora, retire una a una las pesas de la porta pesas. Anote las posiciones x2 correspondientes y complete la tabla 1.
Recuerde que:
Grafique la magnitud de la fuerza F versus la elongación media. Aplicando el método de mínimos cuadrados encuentre la curva de mejor ajuste
Interprete físicamente la curva que encontró:
Se observa en el gráfico que existe una relación directamente proporcional entre la fuerza ejercida por el porta pesas y la elongación del resorte
Determine la constante elástica k del resorte;
K= 27.49
|
TABLA 1 |
||||||
|
N° |
m (kg) |
X1 (m) |
X2 (m) |
X (m) |
F (N) |
K (N/m) |
|
1 |
0.05 |
0.01 |
0.012 |
0.011 |
0.49 |
- |
|
2 |
0.1 |
0.028 |
0.029 |
0.0285 |
0.98 |
28 |
|
3 |
0.15 |
0.045 |
0.048 |
0.0465 |
1.47 |
27.2 |
|
4 |
0.2 |
0.065 |
0.066 |
0.0655 |
1.96 |
25.78 |
|
5 |
0.25 |
0.083 |
0.083 |
0.083 |
2.45 |
28 |
|
6 |
0.3 |
0.1 |
0.102 |
0.101 |
2.94 |
27.2 |
|
7 |
0.35 |
0.12 |
0.12 |
0.12 |
3.43 |
25.78 |
MONTAJE 2
Para este caso seguimos los siguientes pasos:
1. Medimos las dimensiones geométricas de la regla metálica:
Longitud (L): 0,63 m
Ancho (a): 0,0246 m
Espesor (b): 9 x 10-4 m
2. Colocamos la regla en posición horizontal, apoyándola de modo que las marcas grabadas cerca de los extremos de ésta descansen sobre las cuchillas.
3. Determinamos la posición inicial del centro de la varilla con respecto a la escala vertical graduada.
Posición inicial: 0.902 m
4. Fuimos cargando gradualmente la varilla, por su centro, y midiendo las flexiones correspondientes (s’). Anotamos los resultados en la tabla 2
5. Una vez que consideramos haber obtenido una deformación suficiente, descargamos gradualmente la varilla, midiendo y anotando las flexiones correspondientes (s’’).
6. Con los resultados obtenidos, calculamos el valor promedio de los pares de s’ y s’’ para cada carga y lo anotamos en la tabla 2.
N°
Carga m (Kg)
S’ (mm)
S’’ (mm)
S (mm)
1
0.02
3
3
3
2
0.04
6
6
6
3
0.06
8
8
8
4
0.08
10.1
10
10.5
5
0.1
12
12
12
6
0.12
15
15
15
7
0.14
17
17
17
DONDE : S es el promedio de s’ y s’’
V- EVALUACION
1.- Con los datos de la tabla 1, determinar la constante elástica en forma analítica.
|
Nº |
m(Kg) |
x1(m) |
x2(m) |
x'(m) |
F(N) |
|
1 |
0.05 |
0.01 |
0.012 |
0.011 |
0.49 |
|
2 |
0.1 |
0.028 |
0.029 |
0.0285 |
0.98 |
|
3 |
0.15 |
0.045 |
0.048 |
0.0465 |
1.47 |
|
4 |
0.2 |
0.065 |
0.066 |
0.0665 |
1.96 |
|
5 |
0.25 |
0.083 |
0.083 |
0.083 |
2.45 |
|
6 |
0.3 |
0.1 |
0.102 |
0.101 |
2.94 |
|
7 |
0.35 |
0.12 |
0.12 |
0.12 |
3.43 |
5. Determinar el Keq para resortes colocados en serie y paralelo respecto a una masa.
Resortes en serie: Se denomina como sistema de resortes en serie al sistema compuesto por dos o más resortes que reciben una fuerza común y se encuentran conectados unos a otros en un extremo como se muestra en la figura:
En un sistema de n resortes, la elongación Δx de cada uno, por la ecuación 1 sería igual a:
Entonces la deformación total del sistema (despreciando el espacio que pudieran ocupar las conexiones entre resortes) estaría dado por:
Debido a que la fuerza soportada por todo el sistema es igual a F, la constante de elasticidad del sistema sería igual a:
Resortes en paralelo: Se conoce como sistema de resortes en paralelo, al sistema formado por dos o más resortes conectados a una misma masa sin tener ningún nodo común entre ellos, sin embargo, todos sus nodos deben estar en una misma línea del espacio, como se muestra en la figura:
Una de las principales características de este sistema, es que, bajo condiciones ideales, todos los resortes se alargan en igual medida. De esta propiedad se puede saber que la fuerza total ejercida al sistema es igual a:
Entonces la constante de recuperación total sería igual a:
6. Analice la razón existente de la diferencia de la constante elástica de dos diferentes resortes en espiral
La razón por la cual la constante elástica de dos resortes diferentes es distinta es porque ésta posee un valor único que nos permite diferenciar y caracterizar los resortes, pues un resorte hecho de acero va a tener una constante elástica mayor que uno hecho de cobre ya que éste opone menor resistencia al estiramiento o compresión, lo cual demuestra que el material del que están hechos condicionan sus propiedades elásticas y con ellas su constante de elasticidad.
7. Analizar y verificar la diferencia existente entre un muelle tipo espiral y un muelle tipo laminar o de banda
Muelle tipo laminar
Está formado por una serie de láminas de acero de sección rectangular de diferente longitud, las cuales trabajan a flexión; la lámina de mayor longitud se denomina lámina maestra. Las láminas que forman la ballesta pueden ser planas o curvadas en forma parabólica, y están unidas entre sí. Por el centro a través de un tornillo o por medio de una abrazadera sujeta por tornillos.
Se utiliza como resortes de suspensión de vehículos teniendo una finalidad de amortiguar los impactos de accidentes vehiculares.
Muelle en espiral
Es un resorte de torsión que requiere muy poco espacio axial, está formado por una lámina de acero de sección rectangular enrollada en forma de espiral.
Se utiliza para producir movimiento en mecanismos de relojería, cerraduras, persianas, metros enrollables, juguetes mecánicos, etc.
8. ¿Por qué el esfuerzo a la tracción es positivo y el esfuerzo a la compresión es negativa?
Tenemos que tener en cuenta primero que el esfuerzo es la fuerza que actúa sobre un cuerpo y que tiende a estirarla (tracción), aplastarla (compresión),etc.
Entonces podemos analizar el esfuerzo (f) mediante la ley de Hooke para un muelle o resorte, donde:
F=KX
Entonces para una tracción (estiramiento), nuestro x será positivo, por el cual nuestro esfuerzo será también positivo. En cambio, para una compresión nuestro valor de x tomará un valor negativo, por el cual nuestro esfuerzo será negativo.
9. Analice las fuerzas de cohesión y fuerzas de adherencia. Dé ejemplos.
Solución n°9:
1. Fuerzas de Cohesión:
Las fuerzas de cohesión son fuerzas que atraen y unen a las moléculas de la misma clase. Como moléculas de líquidos, solidos o gases.
En palabras simples las fuerzas de cohesión vienen a ser las fuerzas encargadas de unir las moléculas de los distintos compuestos que existen.
Como ejemplo de fuerzas de cohesión tenemos:
- En el caso de un líquido como el agua las fuerzas de cohesión entre sus moléculas de agua vienen a ser las fuerzas intermoleculares (Puente de hidrogeno).
2. Fuerzas de adhesión:
Las fuerzas de adhesión son aquellas fuerzas que se dan entre moléculas de diferentes clases mediante fuerzas intermoleculares. Estas se pueden dar por ejemplo entre líquidos y sólidos.
Como ejemplo de fuerzas de adhesión tenemos:
- Una gota de agua adhiriéndose a una telaraña
- El cemento adhiriéndose al ladrillo.
10.- Determine para la regla metálica el valor del módulo de Young (E) en N⁄m^2 .
|
s (mm) |
F(N) |
s.F |
s**2 |
|
3 |
0.196 |
0.588 |
9 |
|
6 |
0.392 |
2.352 |
36 |
|
8 |
0.588 |
4.704 |
64 |
|
10.05 |
0.784 |
7.879 |
101 |
|
12 |
0.98 |
11.76 |
144 |
|
15 |
1.176 |
17.64 |
225 |
|
17 |
1.372 |
23.324 |
289 |
| Sumatoria: |
71.05 |
5.488 |
68.247 |
868 |
Numero de términos: n=7
Ecuación de la recta: F=ms+b
Por formula:
F/s=(4Eab^3)/L^3
Ancho: a=24.6mm
Longitud: L=63mm
Espesor: b=0.9mm
11.- ¿Cuánto vale la energía elástica acumulada en la barra del experimento 2 en su máxima deformación?
Solución n°11:
El experimento número 2 se muestra a continuación:
Nosotros sabemos que la energía potencial elástica viene dada por la ecuación:
E = 1/2⋅kx^2
Donde:
k= Constante elástica de la barra.
x= Deformación de la barra.
De nuestra tabla de informaciones numero 2 podemos observar que la máxima deformación que ha tenido nuestra barra es de 17 milímetros.
Por lo tanto:
X(max)= 17mm ………………. (1)
Solo nos falta hallar la constante elástica de la barra (k), sabemos que la constante elástica de todo material depende de las dimensiones geométricas de este y de su módulo de Young (E).
K= 1/4E⋅L^3/(ab^3 )
Donde:
E: Modulo de Young
L: Longitud de la barra
a: Ancho de la barra
b: espesor de la barra
Conociendo los datos y remplazando en la formula obtendremos la constante elástica de la barra.
Por lo tanto:
K = 11.7 N/m………………. (2)
Usando la ecuación (1) y la ecuación (2) y remplazando en la ecuación de la energía potencial elástica obtendremos:
Por lo tanto, la energía potencial elástica con la deformación máxima viene dada por:
E = 1.69065〖.10〗^(-3)N.m
Conclusiones:
Las conclusiones que hemos llegado tras la experiencia N° 1 son:
- En todo cuerpo que conste de coeficiente elástico su constante elástica depende de las características geométricas de este y su módulo de Young.
- Las fuerzas de cohesión son aquellas encargadas de unir las moléculas de la misma clase brindando ciertas características a los compuestos (como la tensión superficial o el estado de agregación en que se les puede encontrar) y las fuerzas de adhesión aquellas de unir las moléculas de diferente clase.