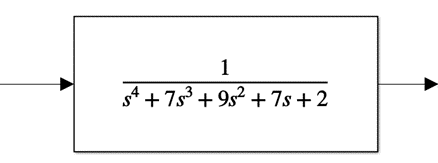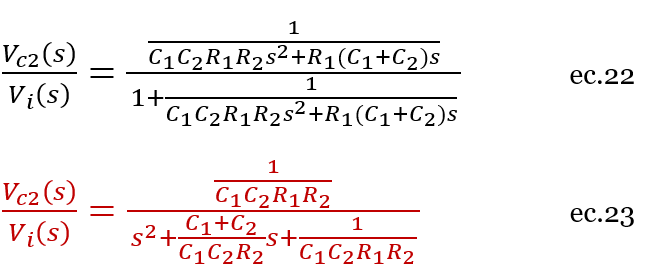Autores: Mauro Benito Montoya Arenas (mauro2017pre@gmail.com)             

                                    Terry Quispe Paniagua (terryfiee2021@gmail.com) 

Representaciones graficas de sistemas de control

Resumen: En el presente documento tiene como objetivo modelar , resolver o simplificar tanto en diagrama de bloques como de flujo , haciendo uso  para el diagrama de bloques ,del traslado de bloques como también las más comunes expresiones de sistemas ,para poder reducir la cantidad de bloques y finalmente se obtuvo la función transferencia T(s) , posteriormente se hizo la conversión de bloques a diagrama de flujo de señales para posteriormente aplicar el método de Mason  de manera procedimental para obtener la expresión total simplificada que debe ser igual a lo obtenido tanto en la simplificación del diagrama de bloques y su repuesta en el tiempo tanto ante una entrada a escalón o impulso de estos debe ser idéntico a la implementación en Matlab /Simulink , lo cual se demuestra , detalla y explica satisfactoriamente en el presente.

I. INTRODUCCION

En la actualidad muchos de los sistemas que nos rodean fueron construidos a partir de un diagrama para describir su funcionamiento interno, siendo parte y apoyado de las leyes físicas expresadas en ecuaciones dinámicas que reflejan el comportamiento de dicho sistema, tales son los casos conocidos como diseño de plantas de control, aparatos como drones, autos, procesos industriales, etc.

Por lo cual es de suma importancia para el estudiante conocer sobre cómo se modelan sistemas y simplifican para poder hallar su función de transferencia, para ello es necesario conocer el comportamiento físico del sistema y aplicar las leyes físicas que intervienen en dicho sistema. Además, para su simplificación o hallar la función de transferencia se utilizará tanto reducción por el álgebra de bloques como el método de masón.

Estos 2 métodos cada uno con sus propias características de desarrollo pero que conducen a una misma respuesta, la cual podremos someter a evaluación mediante el software de Matlab/Simulink, es decir definir una entrada como por ejemplo las más conocidas que son el escalón unitario(step) o impulso para posteriormente ver el comportamiento en el tiempo del sistema.:

II. MARCO TEORICO

DIAGRAMA DE BLOQUES: 

Un diagrama de bloques de un sistema es una representación gráfica de las funciones que lleva a cabo cada componente y el flujo de señales, este diagrama muestra las relaciones existentes entre los diversos componentes. A diferencia de una representación matemática puramente abstracta .en el diagrama de bloques todas las variables en un sistema son relacionadas y se enlazan por medio de bloques funcionales , el bloque es una representación de una operación matemática que hace a la señal de entrada producir una salida[1,p. 17], una de las ventajas más importantes de este diagrama es que es fácil de formar mediante las ecuaciones dinámicas que describen el comportamiento de un sistema como ya hemos visto podemos conectar bloques de componentes de acuerdo al flujo de señales y también es posible evaluar internamente la contribución de cada componente a diferencia de tener el bloque resultante del sistema ya simplificado por el álgebra de bloques o de manera analítica, en síntesis el diagrama de bloques es una representación gráfica y abreviada de la relación causa y efecto entre la entrada y salida de un sistema físico[2,p. 18] . La fig. 1 muestra un elemento del diagrama de bloques, esta tiene una entrada y una salida, en donde la entrada es por donde entra la flecha y por donde sale es naturalmente la salida.

Figura 1 Elemento de un diagrama de bloques

BLOQUES EN SERIE O CASCADA:

Estos bloques llamados en serie por algunos autores [3] o cascada [2] se conectan de la misma manera como se aprecia en la fig. 2, obviamente esto se puede extender hasta n bloques que pueden ser distintos, es decir diferentes operaciones en donde la entrada se va a operar con los bloques mediante el producto para producir la salida, en la fig. 3 se muestra el bloque resultante de la cascada de la fig. 2.

Figura 2 Bloques en cascada

Figura 3 Bloque resultante

BLOQUES EN PARALELO

Este tipo de sistema son aquellos que nacen desde un mismo punto, es decir tienen una misma entrada para posteriormente sumarse  o restarse por medio de un pequeño circulo , llamado punto de suma , con el signo apropiado más o menos , asociados a las flechas que entran al círculo para posteriormente obtener una salida , algunos autores ponen una cruz en lugar del punto suma que se muestra en la fig. 4 [3], la fig. 4 ilustra este tipo de sistema en donde se puede reducir a un único bloque que será la suma de estos como se aprecia en la fig.5.

Figura 4 Bloques en paralelo

Figura 5 Bloque resultante

FUNCION DE TRANSFERENCIA

La función de transferencia de un sistema descrito mediante una ecuación diferencial lineal e invariante en el tiempo se define como el cociente entre la transformada de Laplace de la salida (función de respuesta) y la transformada de Laplace de la entrada (función de excitación) bajo la suposición de que todas las condiciones iniciales son cero [5,p. 626].

Si consideramos un sistema lineal e invariante en el tiempo descrito mediante la siguiente ecuación diferencial:

En donde la salida y la entrada son y, x respectivamente. entonces la función de transferencia de este sistema es cociente de la transformada de Laplace de la salida y la transformada de Laplace de la entrada mostrada en la ecuación 2, cuando las condiciones iniciales son cero, a partir de esta ecuación se puede representar la dinámica de muchos sistemas en donde el denominador define el orden del sistema 

RETROALIMENTACION NEGATIVA O FEEDBACK

Uno de las configuraciones más importantes, por su aplicación a las sistemas de control, a diferencia de las simplificaciones obvias anteriores en este sistema es conveniente definir puntos para obtener el bloque resultante , como se muestra en la fig. 6.

Figura 6 Bloques en feedback

Sea el bloque superior G(s) y el bloque inferior H(s)

Analizando el diagrama podemos hacer ecuaciones que nos ayudaran a simplificar la expresión en un solo bloque

Y(s)=E(s)G(s) ec. 3

E(s)=R(s)-B(s) ec.4

B(s)=Y(s)H(s) ec.5

Sustituyendo la ec.5 en ec.4 y reemplazando en la ec.3 obtenemos:

Y(s)=R(s)G(s)-G(s)[Y(s)H(s)] ec.6

Factorizando Y(s):

Y(s)[1+G(s)H(s)]=R(s)G(s) ec.7

Finalmente:

Y(s)/R(s) =G(s)/(1+G(s)H(s) ) ec.8

La ec.8 es la función de transferencia del sistema de realimentación negativa mostrado , en el caso de que H(s) sea la unidad será un sistema con retroalimentación unitaria.

DIAGRAMA DE FLUJOS:

También llamado grafico de flujo de señal SFG [3] o  DFS[2], a diferencia del diagrama de bloques estos se caracterizan por tener puntos unión , o nodos , se utilizan para representar variables. Los nodos están conectados por segmentos lineales llamados ramas , de acuerdo a las ecuaciones de causa y efecto[3,p. 89] , por ejemplo si consideramos un sistema lineal simple como la ecuación:

Y(s)=G(s)R(s) ec.9

La representación en SFG de la ec.9 se observa en la fig. 7.

Figura 7 SFG

Observamos la entrada R(s) se dirige al nodo Y(s) expresando dependencia de las salida respecto a la entrada , pero no al revés.

Propiedades de las SFG:

1. La SFG se aplica solamente a sistemas lineales.

2. Las ecuaciones a partir de las cuales se dibuja una SFG deben ser algebraicas en la forma de causa y efecto.

3. Los nodos se utilizan para expresar variables.

Relación existente entre diagrama de bloques y diagrama de flujo se muestra a continuación en la fig. 8, posteriormente la relación entre punto de suma y punto de reparto entre estos 2 diagramas se muestra en la fig.9.

Figura 8 Relación entre bloque y rama

Figura 9 Relación entre punto suma y punto de reparto

REDUCCION DE DIAGRAMA DE FLUJO DE SEÑALES (METODO DE MASON)

La finalidad de representar un sistema de control en DFS o DB no sólo es proveer una representación gráfica de las relaciones entre variables y subsistemas procedentes de un conjunto de ecuaciones; también debe hacer posible obtener una función de transferencia equivalente (en forma de función racional formada por un único numerador y un único denominador, ya sea en forma de bloque o de rama) a la que por su importancia se le llamará función de transferencia de lazo cerrado y que está representada por T(s) [2,p. 145].

Este método es un procedimiento mediante el cual podemos calcular u obtener la función de transferencia T(s) de sistemas SISO o MIMO el procedimiento se muestra a continuación.

El procedimiento de Mason se define con la ec.10.

TRAYECTORIA: 

Una trayectoria es cualquier recorrido unidireccional que va desde la entrada hasta la salida; al recorrerla, no es posible pasar por un mismo nodo más de una vez (esto es para evitar recorridos cerrados que se definirán luego como ciclos).

- Ganancia de trayectoria: Es el producto de las funciones de transferencia individuales que forman cada trayectoria.

CICLO: Un ciclo es todo recorrido unidireccional cerrado que empieza y termina en el mismo nodo, de manera tal que al recorrerse no es posible pasar por un mismo nodo más de una vez.

- Ganancia de ciclo: Es el producto de las funciones de transferencia individuales que componen cada ciclo.

DETERMINANTE: 

Para evaluar el determinante ∆ del DFS respectivo es necesario el siguiente concepto:

Dos ciclos se tocan entre sí cuando éstos tienen en común un mismo nodo; en caso contrario, se dice que los ciclos no se tocan entre sí. De esta manera la determinante se define por la ec.11.

COFACTOR: 

Se considera que un ciclo y una trayectoria se tocan entre sí cuando ambos tienen en común un mismo nodo. Este concepto se utiliza para definir el cofactor asociado a cada trayectoria (habrá tantos cofactores como trayectorias). El cofactor de una trayectoria es el determinante del DFS formado por la supresión de todos los ciclos que toquen a la trayectoria bajo consideración. El cofactor se define en la ec.12.

∆_1=1-(suma de las ganancias de todos los ciclos que no tocan la trayectoria considerada)+ (suma de los productos de las ganancias de todas las  combinaciones de dos ciclos que no toquen a la trayectoria considerada y que no se toquen entre sí) - (suma de los productos de las ganancias de todas las combinaciones de tres ciclos que no toquen a la trayectoria considerada y que no se toquen entre sí) +⋯ ec.12

Finalmente, una vez obtenido todas estas componentes reemplazamos en la ec.10 y obtenemos T(s) [2,p.146-150].

ANALISIS DE CIRCUITOS:

Para analizar un circuito se opta por transformar del dominio temporal al dominio de la variable laplaciana s, en donde podemos convertir a los operadores (derivadas o integrales) en multiplicadores como ya conocemos s y 1/s .Esto facilita el cálculo a través del uso de las leyes de Kirchoff ,para obtener expresiones que faciliten el álgebra para finalmente poder construir el diagrama de bloques [5,p.623]. Se conocen 2 caminos el trabajar en el dominio temporal y luego pasar las expresiones a Laplace o transformar al circuito directamente a Laplace.

II. MATERIALES Y METODOS   

A. EQUIPOS, MATERIALES Y HERRAMIENTAS UTILIZADAS

Figura 10. Software Matlab

Figura 11. Software Simulink

B. ESQUEMAS

Figura 12. Circuito eléctrico en serie

Figura 13. Diagrama de bloques para el circuito RC

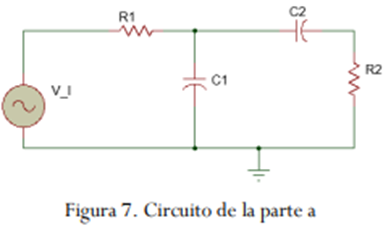
Figura 14.  Circuito de la parte a

Figura 15. Circuito de la parte a implementado en diagrama de bloques

Figura 16. Circuito de la parte a implementado en diagrama de flujos

Figura 17. Se muestra el circuito de la parte “a” caso2

Figura 18. Circuito de la parte “a” caso 2 implementado en diagrama de bloques

Figura 19. Circuito de la parte “a” caso 2 implementado en diagrama de flujos

Figura 20. Circuito de la parte “b” implementado en diagrama de bloques

Figura 21. Circuito de la parte “b” implementado en diagrama de flujos

Figura 22. Circuito del cuestionario final implementado en diagrama de bloques

Figura 23. Circuito del cuestionario final implementado en diagrama de flujos

C. PROCEDIMIENTO

Para el desarrollo de la guía deberá fijar un determinado valor de R1, R2, C1, C2. 

a.      En base al circuito que se presenta en la figura 7, realice los siguientes pasos:

Figura 24. Circuito de la parte a

Consideramos: R_1=500Ω,R_2=700Ω,C_1=10uF,C_2=80uF

i.                    Considerando como señal de entrada al voltaje Vi y como señal de salida al voltaje en el capacitor C2. Presente el diagrama de bloques del sistema en Simulink. 

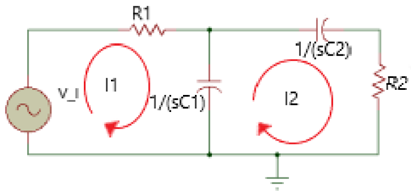
El circuito expresado en Laplace será:

Figura 25. Se muestra las corrientes que pasan por las mallas y el circuito en el dominio de laplace

Expresado en diagrama de bloques:

Figura 26. Diagrama de bloques con V_i (s) de entrada y V_c2 (s) de salida

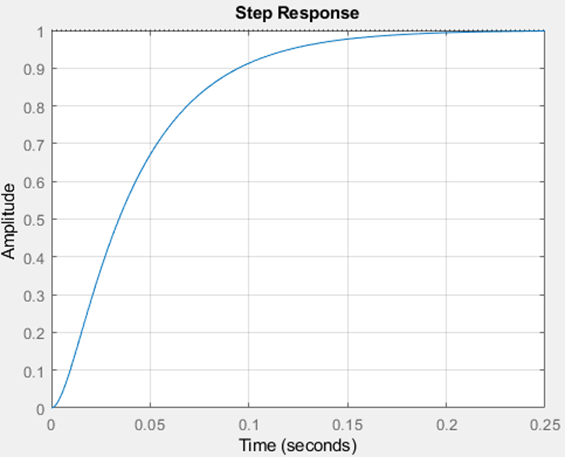
ii.                    Muestre la respuesta temporal del sistema ante una entrada escalón unitario (Matlab/Simulink)

Figura 27. Creamos el fichero para la simulación

Figura 28. Señal de salida ante una entrada escalón

Simulink

Figura 29. Grafica superior: Señal escalón Vi(s), grafica inferior: Señal de salida Vc2(s)

iii.                    Mediante el álgebra de bloques, realice la simplificación para obtener una función de transferencia equivalente.

De la figura 26:

Figura 30. Simplificación del diagrama de bloque de la figura 26

Podemos ver que existe una retroalimentación. Entonces:

Figura 31. Función de transferencia del sistema

iv.                    Obtener la respuesta temporal de esta función simplificada, hallada en iii, ante una entrada escalón y compárela con las obtenidas en el punto ii. ¿Son diferentes? Realice comentarios. 

La función de transferencia reemplazando los valores de R_1=500Ω,R_2=700Ω,C_1=10uF,C_2=80uF, quedaría:

Matlab 

Figura 32. Creamos el fichero para la simulación

Figura 33. Señal de salida ante una entrada escalón

Simulink

Figura 34. Grafica superior: Señal de salida Vc2(s), grafica inferior: Señal escalón Vi(s)

Comparación con la gráfica obtenida en el punto ii

Figura 35. Diagrama de bloques obtenido de las ecuaciones del circuito (parte superior), diagrama de bloques obtenido de la función de transferencia (parte inferior)

Figura 36. Señal de salida para el diagrama de bloques del punto ii (grafica superior), Señal de salida para el diagrama de bloques del punto iii (grafica inferior)

Comentarios

En el punto ii hallamos el diagrama de bloques a partir de las ecuaciones generadas en el sistema. En el punto iii hallamos el diagrama de bloques utilizando algebra de bloques para simplificar el diagrama del punto ii. Es decir que ambos diagramas son los mismos, solo que el diagrama del punto iii esta simplificado. Por eso, la señal de salida debe ser la misma en ambos casos, ya que hemos cambiado la configuración de los bloques pero es producto de una simplificación y la salida no se ve alterada.

v.                    Cómo se podría realizar esta simplificación usando comandos de Matlab. 

Para realizar la simplificación se podría usar la función “feedback” que ya usamos en el punto ii.

Figura 37. Simplificación de bloques usando “feedback”

Figura 38. Señal de salida ante una entrada escalón

vi.                    Presente el diagrama de flujo correspondiente al sistema descrito en i. 

El sistema expresado en diagrama de flujos será: 

Figura 39. Diagrama de flujos del sistema

Aplicando la ley de Mason:

La función de transferencia reemplazando los valores de R_1=500Ω,R_2=700Ω,C_1=10uF,C_2=80uF, quedaría:

(V_c2 (s))/(V_i (s) )=(2500/7)/(s^2+1125/7 s+25000/7) ec.32

Ahora utilice adecuadamente la función SolucionMason.m para obtener la función de transferencia simplificada. ¿Se obtuvo el mismo resultado que en iii y en su Informe Previo? 

Figura 40. Se crea el archivo .net que contendrá los valores de los bloques del diagrama y se reemplaza R_1,R_2,C_1  y C_2 por sus valores elegidos

Figura 41. Introducimos el archivo ”caso_avii_Guia4 .net” en la entrada, así también el nodo de inicio (1) y el nodo final(5)

Figura 42. Resultado de la función de transferencia hecho por la función “SolucionMason.m” después de introducir como entrada el archivo .net generado

Análisis

Podemos ver que la función de transferencia generada por la función “SolucionMason.m” es la misma que obtuvimos haciendo el análisis matemático (la única diferencia es que el numero 7 pasa como denominador en la función de transferencia que nosotros obtuvimos). Lo que corrobora que nuestro resultado es verdadero.

Función de transferencia generado por la función “SolucionMason.m”:

Ahora considerando como señal de entrada el voltaje Vi y como señal de salida al voltaje en la resistencia R2, presente el diagrama de bloques respectivo. ¿Es muy diferente al obtenido en i? Realice comentarios. 

Figura 43. Se muestra el circuito de la parte “a” pero con la salida V_R2 (t) especificada

El circuito expresado en Laplace será:

Figura 44. Se muestra las corrientes que pasan por las mallas y el circuito en el dominio de laplace

Figura 45. Diagrama de bloques con V_i (s) de entrada y V_R2 (s) de salida

Comentarios

El diagrama de bloques obtenido es diferente al que obtuvimos en la parte i. Cambia la forma de expresar la corriente I2(s) (ahora es una función de segundo orden ya que existen 2 capacitores). Después a la corriente se le multiplica por la constante R2 para que te dé el valor del voltaje V_R2 (s)

ix.                    Vuelva a realizar los pasos ii, iii, iv, v, vi y vii para este nuevo sistema. 

ii.2. Muestre la respuesta temporal del sistema ante una entrada escalón unitario (Matlab/Simulink) 

Matlab

Figura 46. Creamos el fichero para la simulación

Figura 47. Señal de salida ante una entrada escalón

Simulink

Figura 48. Grafica superior: Señal de salida Vr2(s), grafica inferior: Señal escalón Vi(s) 

iii.2. Mediante el álgebra de bloques, realice la simplificación para obtener una función de transferencia equivalente. 

De la figura 45:

Figura 49. Simplificación del diagrama de bloque de la figura 45

Podemos ver que existe una retroalimentación. Entonces:

Figura 50. Función de transferencia del sistema

iv.2. Obtener la respuesta temporal de esta función simplificada, hallada en iii.b, ante una entrada escalón y compárela con las obtenidas en el punto ii. ¿Son diferentes? Realice comentarios. 

La función de transferencia reemplazando los valores de R_1=500Ω,R_2=700Ω,C_1=10uF,C_2=80uF, quedaría:

(V_c2 (s))/(V_i (s) )=200s/(s^2+2525/7 s+25000/7) ec.48

Matlab

Figura 51. Creamos el fichero para la simulación

Figura 52. Señal de salida ante una entrada escalón

Simulink

Figura 53. Grafica superior: Señal de salida Vr2(s), grafica inferior: Señal escalón Vi(s)

Comparación con la gráfica obtenida en el punto ii

Figura 54. Diagrama de bloques obtenido de las ecuaciones del circuito (parte superior), diagrama de bloques obtenido de la función de transferencia (parte inferior)

Figura 55. Señal de salida para el diagrama de bloques del punto ii (grafica superior), Señal de salida para el diagrama de bloques del punto iii (grafica inferior)

Comentarios

En el punto ii.2 hallamos el diagrama de bloques a partir de las ecuaciones generadas en el sistema (considerando en este caso Vr2(s) como salida en lugar de Vc2(s)). En el punto iii.2 hallamos el diagrama de bloques utilizando algebra de bloques para simplificar el diagrama del punto ii.2. Es decir que ambos diagramas son los mismos, solo que el diagrama del punto iii.2 esta simplificado. Por eso, la señal de salida debe ser la misma en ambos casos, ya que hemos cambiado la configuración de los bloques, pero es producto de una simplificación y la salida no se ve alterada. En la gráfica se puede observar lo que se está explicando. Pues la forma de la señal de salida es invariante.

v.2. Cómo se podría realizar esta simplificación usando comandos de Matlab. 

Para realizar la simplificación se podría usar la función “feedback” que ya usamos en el punto ii.

Figura 56. Simplificación de bloques usando “feedback”

Figura 57. Señal de salida ante una entrada escalón

vi.2. Presente el diagrama de flujo correspondiente al sistema descrito en i.b.

El sistema expresado en diagrama de flujos será: 

Figura 58. Diagrama de flujos del sistema

vii.2. Ahora utilice adecuadamente la función SolucionMason.m para obtener la función de transferencia simplificada. ¿Se obtuvo el mismo resultado que en iii y en su Informe Previo? 

 

Figura 59. Se crea el archivo .net que contendrá los valores de los bloques del diagrama y se reemplaza R_1,R_2,C_1  y C_2 por sus valores elegidos

Figura 60. Introducimos el archivo ”caso_avii_Guia4 .net” en la entrada, asi también el nodo de inicio (1) y el nodo final(5)

Figura 61. Resultado de la función de transferencia hecho por la función “SolucionMason.m” después de introducir como entrada el archivo .net generado

Análisis:

Podemos ver que la función de transferencia generada por la función “SolucionMason.m” es la misma que obtuvimos haciendo el análisis matemático (la única diferencia es que el numero 7 pasa como denominador en la función de transferencia que nosotros obtuvimos). Lo que corrobora que nuestro resultado es verdadero. Por ejemplo. En la parte del numerador si multiplicamos 200x7 nos quedaría 1400.

Función de transferencia obtenida de la función “SolucionMason.m”:

H(s)=1400s/(〖7s〗^2+2525s+25000) ec.57

Función de transferencia obtenida de forma analítica:

H(s)=200s/(s^2+2525/7 s+25000/7) ec.58

x.                    Documente y describa la implementación y los resultados obtenidos.

Descripción:

En esta parte (parte a) del informe hemos hallado primero el diagrama de bloques y el diagrama de flujos a partir del circuito, después hemos hallado la función de transferencia de las 2 formas posibles: a partir del diagrama de bloques y a partir del diagrama de flujos. Con los resultados obtenidos hemos simulado (en Matlab y en Simulink) para comprobar nuestros resultados y compararlos. Además, hemos utilizado la función “SolucionMason” para tener la función de transferencia hecha a través de la ley de Mason y comprobar con nuestros resultados. Todo esto lo hicimos para 2 tipos de salida: Primero se hizo un análisis cuando la salida era Vc2(s) (en el capacitor C2) y después cuando la salida era Vr2(s) (en la resistencia R2). En el primer caso el voltaje tenía que aumentar conforme pasaba el tiempo ya que era un capacitor, y en el segundo caso el voltaje tenía que disminuir ya que se trataba de una resistencia y el capacitor absorbía mas voltaje conforme pasaba el tiempo.

b.      Considerando el diagrama de la figura 8, donde:

G_1 (s)=1/(1+s),G_2 (s)=2/(s+3),G_3 (s)=(s+4)/(s+5),H_1 (s)=3,H_2=1/(s+2),H_3 (s)=4 ec.59

Figura 62.  Diagrama de la parte b

i.         Realice en Simulink el diagrama de bloques presentado en la figura 8. 

Figura 63. Diagrama de bloques en Simulink

El diagrama está contenido en un archivo Simulink de nombre laboratorio4.slx

ii.         Obtener la respuesta temporal del sistema ante una entrada escalón unitaria (Matlab/Simulink). 

Figura 64.  Respuesta temporal del sistema ante un escalón Simulink

Mediante Simulink visualizamos la respuesta temporal del sistema ante un escalo mediante scope , además de ello para suavizar la grafico usamos las opciones configuración para en donde el la opción de solver selección usamos el fixed step y le damos el tamaño en este caso usamos 0.01 para poder suavizar lo suficiente la gráfica como se muestra en la fig. 12 , los detalles de la configuración se muestran en la fig. 13.

Figura 65. Configuración de solver selection

Figura 66.  Respuesta temporal del sistema ante un escalón Matlab

Para representar la respuesta temporal así como se hizo en Simulink utilizamos la función Step no sin antes definir nuestra función de transferencia de componentes denominador y numerador con la función tf(numerador, denominador).

iii.                     Mediante el álgebra de bloques, realice la simplificación para obtener una función de transferencia equivalente.

Para obtener la función de transferencia equivalente del sistema se utilizo el algebra de bloque para poder reducirlo de esta manera se logra obtener un bloque común el cual esta definido su expresión por la Fig. 15 la cual se implemento en Simulink y se logra apreciar que efectivamente coincide con el análisis del previo , que posteriormente se comprobara. Otra que cosa que notamos es que nuestro sistema es de orden 4 debido al denominador.

Figura 67.  Bloque resultante de la simplificación

iv.                     Obtener la respuesta temporal de la función de transferencia simplificada, hallada en iii, ante una entrada escalón unitario y compárela con las obtenidas en el punto ii. ¿Son diferentes? Realice comentarios.

Puesto que el diagrama simplificado anterior mostrado corresponde al diagrama mostrado en la fig.11 , indudablemente las 2 deben necesariamente tener la misma grafica de respuesta ante la misma entrada como se muestra en la fig. 16 , de no ser así es correcto afirmar que existen errores en la simplificación

Figura 68. Respuesta temporal del sistema ante un escalón Simulink

Podemos notar que la respuesta temporal ante el escalón sigue un comportamiento idéntico al de la fig. 12 , como predijimos, apreciamos también que se estabiliza muy cerca de 0.1 pero antes tiene como un pico que sobrepasa el valor estable antes de ello la pendiente es bastante pronunciada.

v.                     Presente el diagrama de flujo correspondiente al sistema descrito en la figura 10.

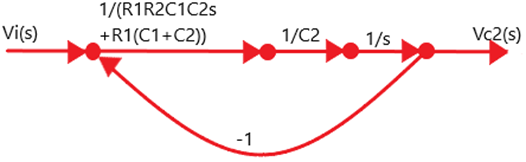
Con las definiciones y equivalencias presentados en la introducción es sencillo poder pasar de diagrama de bloques a diagrama de flujos , esta vez los bloques iran entre nodos las ramas entrantes indicaran una suma , en este caso como la suma es negativa se multiplica la expresión por -1 sin cambiar el sentido de la rama, como se muestra en la fig. 17.

Figura 69. Diagrama de flujo

vi.                     Ahora utilicé adecuadamente la función SolucionMason.m para obtener la función de transferencia simplificada. ¿Se obtuvo el mismo resultado que en iii y en su Informe Previo?

Primero definimos nuestro archivo.net en donde describiremos de una forma que pueda leer el programa y así obtener el resultado que debe ser idéntico a lo obtenido en el previo tanto en diagrama de flujo como de bloques , en este caso el programa realiza la solución por mason para ello en la fig. 17 definimos los nodos del 1 al 6, teniendo en cuenta respetar las posiciones en el orden [coeficiente] [nodo de inicio] [nodo de parada] [valor del coeficiente].

- Primero: Del nodo 1 al 2 hay una ganancia de 1

- Segundo : Del nodo 2 al nodo 3 está la expresión 1/(1+s)

- Tercero: Del nodo 3 al 4 tenemos 2/(s+3)

- Cuarto: Del nodo 4 al 2 está la ganancia -4

- Quinto: Del nodo 4 al 5 tenemos la expresión (s+4)/(s+5)

- Sexto: Del nodo 5 al 3 esta -1/(s+2)

- Séptimo: Del nodo 5 al 2 está la ganancia -3

- Octavo: Del nodo 5 al 6 hay una ganancia de 1

Figura 70. Archivo .net

Figura 71. Resultados del Script Mason.m

Utilizando >> Sys = SolucionMason( 'dfs.net', 1, 6) en comand Windows teniendo guardado el archivo en formato .net y definiendo los nodos en este caso 6 nodos el nodo de inicio 1 y el nodo final 6 , en el resultado podemos notar los datos junto con el resultado en symbolic corroborando así que lo que se obtuvo en el previo es correcto.

Para corroborar definitivamente vamos a definir el resultado Sys que está en symbolic como un tf solo bastara con escribir en el comand Windows >> g=tf(Sys) , para luego aplicarle un escalón step(g) para ver si efectivamente coincide con la gráfica de respuesta presentada anteriormente.

Figura 72. Respuesta ante un escalón de la función resultado del Script Mason.m

Con este grafico de respuesta se concluye definitivamente que la solución es idéntica a las obtenidas por otros métodos como diagramas de flujos o boques como también el resultado obtenido en Simulink.

vii.                     Documente y describa la implementación y los resultados obtenidos.

Es de suma importancia el conocimiento de diagrama de flujo como de bloques los cuales tienen similitudes, por ejemplo, en el diagrama de bloques podemos visualizar con mayor facilidad los elementos que actúan en el diagrama además de poder implementarlo en Simulink y obtener su respuesta, con respecto al diagrama de flujo es relativamente más sencillo de representar, y de poder notar las secuencia con la que interactúan las entradas, en pocas palabras facilita la comprensión. Hemos visto también lo sencillo que resulta pasar de diagrama de bloques a flujo además de simplificar en ambos casos teniendo en cuenta el álgebra de bloques como la solución de mason, en el caso de Mason es una solución regida por sus leyes y tiene un orden definido a diferencia del algebra de bloques, en ambos casos se llega a la misma función transferencia. También resulta importante el fichero Mason.m debido a que facilita el cálculo por la solución de mason solamente debemos definir adecuadamente como se mostró nuestro archivo.net además de definir los nodos de entrada y de salida

III.        ANALISIS DE RESULTADOS

 a.       Considerando el siguiente diagrama de flujo.

Figura 73. Diagrama de flujos del sistema

i.                     Halle su representación en diagrama de bloques.

Figura 74. Diagrama de bloques del sistema

ii.                     Halle su función de transferencia simplificada tanto por diagrama de bloques como por diagrama de flujos. 

Simplificación por diagrama de bloques

Figura 75. Se puede ver en el marco rojo que ahí existe una realimentación

Figura 76. Se puede ver en el marco rojo de la izquierda que ahí existe una realimentación y en el marco rojo de la derecha dos bloques están en serie

Figura 77. Se traslada el bloque 1/(s+1)

Figura 78. Se puede ver en el marco rojo de la izquierda que dos bloques están en serie y en el marco rojo de la derecha dos bloques están en paralelo

Figura 79. Se puede ver en el marco rojo de la izquierda que ahí existe una realimentación y en el marco rojo de la derecha haremos un análisis.

Análisis del marco rojo de la derecha de la figura 79:

Figura 80. Se puede ver que esos 2 bloques dentro del marco están en serie

Figura 81. Simplificación del sistema a través del algebra de bloques

iii.                     Compare las respuestas temporales de los sistemas implementados en i y ii ante una entrada escalón unitaria.

Figura 82. Se muestra en la parte superior el sistema en diagrama de bloques y abajo el bloque que contiene la función de transferencia

Figura 83. Grafica superior: Se muestra la señal de respuesta a partir del diagrama de bloques de la figura 74. Grafica inferior: Se muestra la señal de respuesta a partir de la función de transferencia

Análisis:

Observar la señal de respuesta a partir del diagrama de bloques y a partir de la función de transferencia nos ha ayudado a comprobar nuestros resultados, ya que es inverosímil que ambas graficas sean iguales. Si no son iguales significa que hemos analizado mal el diagrama y la función de transferencia encontrada es errónea.

 iv.                     Intente describir el sistema utilizando comandos de Matlab.

Figura 84. Hallamos los nodos del diagrama de bloques para su análisis en Matlab

Figura 85. Se muestra el código generado para resolver el diagrama de bloques a través de Matlab

Figura 86. Hallamos la función de transferencia a partir del fichero creado en Matlab

Figura 87. Respuesta de la función de transferencia Hs generada del fichero

(Adicional) Función de transferencia usando la función SolucionMason.m

Figura 88. Creamos el archivo “cuestionariofinal_guia4.net” que contendrá la función de Laplace en cada nodo

Figura 89. Ejecutamos el programa “SolucionMason.m” dándole como entrada el archivo .net creado y el no de inicio y el nodo final

Figura 90. Función de transferencia del sistema obtenido a partir de la función “SolucionMason.m”

Análisis:

A través de la función Hs generada por el fichero podemos corroborar que nuestro análisis es correcto. Ya que coinciden, con la particularidad de que la Hs extraída del fichero está dividida entre 18, si dividimos por esa cantidad nuestra función de transferencia hallada a través del análisis de diagrama de bloques y de flujos coincidirán perfectamente.

La ec.81 es la que esta expresado como resultado en el fichero.

En el caso de la solución de la función de transferencia obtenida de la función “SolucionMason.m” podemos aplicar la función “minreal()” para expresar H(s) como la tenemos expresada en la solución hecha a través de Matlab.

Figura 91. Función de transferencia obtenida de la función “SolucionMason.m” aplicando después “minreal()” a Hs, para expresar la respuesta como la obtenida en Matlab

IV.               CONCLUSIONES

- Para simplificar un sistema por el método de Mason es necesario conocer los conceptos de los elementos de la expresión que dará el resultado la función transferencia, cabe resaltar que este método es sistemático, es decir solo existe un camino para hallar la respuesta. Por eso, el diagrama de flujos es un análisis más matemático que analítico, ya que existe una ley (la ley de Mason) que la tenemos que necesariamente la tenemos que usar si queremos hallar la función de transferencia

- Es vital para desarrollar la simplificación en diagrama de bloques saber el álgebra de bloques, un sistema en este método es posible hacerlo de diversas maneras concluyendo en un mismo resultado. Por eso, no hay una única forma de hallar la función de transferencia a partir del diagrama de bloques ya que se puede realizar un paso después del otro si es que el diagrama así lo permite. Este es un método más analítico que matemático.

- Comparando la señal de salida de un diagrama de bloques con su señal de salida a partir de la función de transferencia podemos comprobar si dicha función de transferencia es correcta o incorrecta (ambas graficas deben ser iguales

- Aprendimos las diferencias existentes entre los diagramas de flujos y de bloques, el resultado en cualquiera concluye a una misma respuesta

- El software de Simulink permite expresar el diagrama de bloques y obtener su respuesta dependiendo de la entrada en forma gráfica de manera sencilla.

- El archivo SoluciónMason.m es realmente útil si se desea desarrollar un diagrama de flujos, solo es necesario definir el esquema de flujo en un archivo .net

V.        REFERENCIAS

[1] Katsuhiko Ogata ,Ingenieria de control moderna , Pearson - Prentice Hall , Quinta edición  , pp 17-19 , 2010

[2] Ricardo Hernandez Gaviño , Introducción a los sistemas de control: Conceptos, aplicaciones y simulación con MATLAB , Pearson - Prentice Hall , Primera edición  ,pp. (142-149 , 153-157) , 2010

[3] Benjamin C. Kuo, Sistemas de control automático, Pearson - Prentice Hall , Séptima edición , pp. (78-80, 89-91) , 1996

[4] DiStefno ,Stubberud y Williams , Retroalimentación y sistemas de control , Mc Graw Hill , Segunda edición , p.18 ,1992

[5]Charles K. Alexander | Matthew N.O. Sadiku , Fundamentos de circuitos eléctricos , Mc Graw Hill , Quinta edición , p. (623 , 626) ,2013

VI.        REFERENCIAS BIBLIOGRAFICAS

https://prezi.com/7lsmigqzdj8q/diagramas-de-bloques/

https://la.mathworks.com/matlabcentral/fileexchange/22-mason-m

https://github.com/robwalton/mason