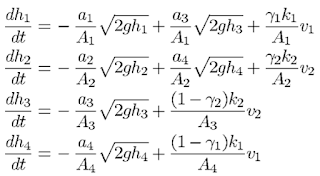Autores: Mauro Montoya Arenas (mauro2017pre@gmail.com)

                   Terry Quispe Paniagua (terryfiee2021@gmail.com)

Modelado de un sistema

I.                   INTRODUCCION

 

SIMULINK es una toolbox especial de MATLAB que sirve para simular el comportamiento de los sistemas dinámicos. Puede simular sistemas lineales y no lineales, modelos en tiempo continuo y tiempo discreto y sistemas híbridos de todos los anteriores. Es un entorno gráfico en el cual el modelo a simular se construye clicando y arrastrando los diferentes bloques que lo constituyen. MATLAB y Simulink trabajan conjuntamente. Cuando utiliza MATLAB y Simulink conjuntamente, en realidad está combinando programación textual y gráfica para diseñar su sistema en un entorno de simulación.

Ingenieros y científicos emplean Simulink para la modelización y la simulación multidominio, ya que es posible reutilizar los modelos en diferentes entornos a fin de simular cómo funcionan todas las partes del sistema juntas. Con Simulink, podrá:

-           Modelizar su sistema en diferentes dominios mediante herramientas específicas y bloques prediseñados.

-          Desarrollar modelos a gran escala mediante el uso de componentes, con librerías y componentes del sistema reutilizables.

-          Combinar sus modelos en una simulación de nivel de sistema, aunque no se hayan creado en Simulink.

-          Ejecutar simulaciones masivas en paralelo en un equipo de escritorio con varios núcleos o en la nube sin tener que escribir montones de código.

II.                MARCO TEORICO

Diagrama de bloques:

Diagrama de bloques es un gráfico que muestra cómo funciona a nivel interno un sistema. Dicha demostración se realiza a través de distintos bloques con sus vínculos, permitiendo de este modo evidenciar la organización del conjunto.

Dicho de otra manera, es un diagrama que represente los diferentes procesos de un sistema. Cada proceso cuenta con bloques, este también posee salidas y entradas en donde los elementos o bloques intermedios se comportarán y producirán diferentes resultados dependiendo de la entrada.

Figura 1. Diagrama de bloques de un sistema de control

 

Función de Heaviside

La función escalón de Heaviside, también llamada función escalón unitario o de causalidad a la derecha del cero. Es una función discontinua cuyo valor es 0 para cualquier argumento negativo, y 1 para cualquier argumento positivo, incluido el cero:

Aplicación: Esta función tiene aplicaciones en ingeniería de control y procesamiento de señales, representando una señal que se enciende en un tiempo específico, y se queda encendida indefinidamente.

Propiedades:

𝑢(−𝑡) = 1 − 𝑢(𝑡)             (ec.2)

𝑢′(𝑡 − 𝑎) = 𝛿(𝑡 − 𝑎)                 (ec.3)

ʆ {𝑢(𝑡 − 𝑎)}(𝑠) = 𝑒−𝑎𝑠 /𝑠               (ec.4)

∫ 𝑢(𝑡 − 𝑎)𝑑𝑡 𝑥 −∞ = 𝑟𝑎𝑚𝑝(𝑥 − 𝑎)       (ec.5)

𝑢(𝑥 − 𝑎) = ∫ 𝛿(𝑡 − 𝑎)𝑑𝑡 𝑥 −∞                      (ec.6)

 

Función rampa

La función rampa es una función elemental real de un solo argumento, continua y diferenciable en todo su dominio excepto en un punto (inicio de la rama) fácilmente computable a partir de la función mínimo o la función valor absoluto. Las principales aplicaciones prácticas de esta función se dan en ingeniería (procesamiento digital de señales, plasticidad, etc.). El término "función rampa" se debe a la forma de su representación gráfica.

Figura 2. función rampa y(x)

¿Qué es una función de transferencia?

Una función de transferencia es un modelo matemático que a través de un cociente relaciona la respuesta de un sistema (modelada o señal de salida) con una señal de entrada o excitación (también modelada). En la teoría de control, a menudo se usan las funciones de transferencia para caracterizar las relaciones de entrada y salida de componentes o de sistemas que se describen mediante ecuaciones diferenciales lineales e invariantes en el tiempo.

Descripción matemática

Uno de los primeros matemáticos en describir estos modelos fue Laplace, a través de su transformación matemática.

Por definición una función de transferencia se puede determinar según la expresión:

H(s)=Y(s)/X(s)                           (ec. 14)

donde H (s) es la función de transferencia (también notada como G (s) ); Y (s) es la transformada de Laplace de la respuesta y X (s) es la transformada de Laplace de la señal de entrada.

La función de transferencia también puede considerarse como la respuesta de un sistema inicialmente inerte a un impulso como señal de entrada:

Cualquier sistema físico (mecánico, eléctrico, etc.) se puede traducir a una serie de valores matemáticos a través de los cuales se conoce el comportamiento de estos sistemas frente a valores concretos.

Por ejemplo, en análisis de circuitos eléctricos, la función de transferencia se representa como:

H(s)=Vout/Vin                                                                    (ec. 18)

 

Bloques comunes de Simulink:

scope:

este bloque sirve para visualizar los diferentes tramos de la simulación pudiendo tener varias señales en pantalla, esto se puede realizar con un mux o ajustar sus parámetros para que cada señal tenga una misma pantalla , además dentro de sus propiedades podemos elegir la escala de tiempo que queremos como también de la amplitud.

Figura 3. Scope de Simulink

clock:

El bloque de reloj emite el tiempo de simulación actual en cada paso de simulación. Este bloque es útil para otros bloques que necesitan el tiempo de simulación. Cuando necesite la hora actual dentro de un sistema discreto, se puede usar el bloque Reloj digital.

Figura 4. Clock de Simulink

mux:

El bloque Mux combina sus entradas en una sola salida. Una entrada puede ser una señal escalar, vectorial o matricial. Dependiendo de sus entradas, la salida de un bloque Mux es un vector o una señal compuesta, es decir, una señal que contiene elementos de matriz y de vector. Si todas las entradas de un bloque Mux son vectores o de tipo vector, la salida del bloque es un vector. Una señal similar a un vector es cualquier señal que es un escalar (vector de un elemento), un vector o una matriz de una sola columna o fila. Si alguna entrada es una señal matricial no vectorial, la salida del bloque Mux es una señal de bus.

Bloque demux

El bloque Demux extrae los componentes de una señal de vector de entrada y emite señales separadas. Los puertos de señal de salida se ordenan de arriba abajo. Los demux tienen 2 puertos:

Input.- Señal de entrada de vector desde la cual el bloque Demux selecciona señales escalares o vectores más pequeños.

Output.- Señales de salida extraídas del vector de entrada. Los puertos de señal de salida se ordenan de arriba abajo

Figura 5. Bloque demux usado en simulink

II.                MATERIALES Y METODOS  

A.       ESQUEMAS

Figura 6. Circuito eléctrico en serie

Figura 7. Circuito de orden superior

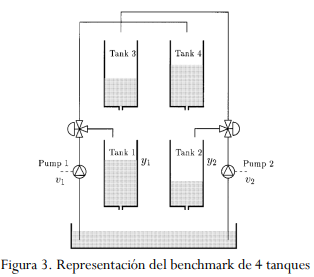
Figura 8. Representación del benchmark de 4 tanques

 

B.       PROCEDIMIENTO

Para el desarrollo de la guía, cada grupo deberá fijar un determinado valor de R, C.

a.       Parte 1. Circuito R-C

Caso 1. Tomando como señal de salida el Voltaje del capacitor:

i.         Defina en Matlab y en Simulink la función de transferencia (ec. 11), la cual representa el comportamiento del sistema considerando como entrada el voltaje de alimentación (u(t)) y como salida el Voltaje generado en el capacitor (Vc(t)).

Función de transferencia:  

Figura 9. Defino la función de transferencia en Matlab

 

Figura 10. Defino la función de transferencia en Simulink

 

ii.                   Simule tanto en Matlab como en Simulink y obtenga la respuesta del voltaje en el capacitor cuando el sistema es sometido a una tensión de entrada de 5 voltios. Comente los resultados. ¿Son los esperados? Justifique su respuesta.

Sea R=5 KΩ, C= 150uF

Figura 11.  Se muestra el circuito RC con los valores predeterminados

 

En nuestro caso: R*C=3/4 : 

Figura 12. Diagrama de bloques de la función de transferencia hecho en simulink 

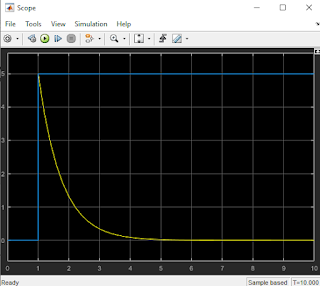
Figura 13. Señal de color azul (señal de entrada), señal de color amarillo (señal de respuesta) en simulink 

Figura 14. Introducimos los datos del valor de la resistencia (R) y la inductancia (L) 

Figura 15. Señal respuesta hecho en Matlab

iii.                 Implemente el circuito R-C (figura 1) y con un osciloscopio observe y documente como el se comporta Vc(t) cuando se aplica u(t)=5 V. Compárela con la obtenida en el punto ii. ¿Es la respuesta esperada? Justifique su respuesta y realice comentarios.

Nota: Debido a que no tenemos acceso a los laboratorios no podemos hacer esta parte de la experiencia.

 

Caso2. Tomando como señal de salida en el Voltaje en la resistencia.

iv.                  De forma analítica, halle la función de transferencia del circuito R-C de la figura 1, considerando como señal de entrada salida el voltaje de alimentación (u(t)) y como señal de salida el voltaje generado en la resistencia (VR(t)).

v.                    Defina la función de transferencia obtenida en (iv) en Matlab y Simulink.

Figura 16. Diagrama de bloques de la función de transferencia hecho en simulink y Matlab

 

vi.                  Simule tanto en Matlab como en Simulink y obtenga la respuesta del voltaje en el resistor cuando el sistema es sometido a una tensión de entrada de 5 voltios. Comente los resultados. ¿Son los esperados? Justifique su respuesta.

Figura 17. Señal de color azul (señal de entrada), señal de color amarillo (señal de respuesta) en simulink

Figura 18. Señal respuesta hecho en Matlab

Análisis: Los resultados obtenidos tanto en Matlab como en simulink son los esperados. Ya que al pasar el tiempo el capacitor va almacenando mas voltaje. A los 4 segundos prácticamente no hay voltaje en la resistencia. Como sabemos τ=RC=4/3, esto quiere decir que a los 1.333 segundos el voltaje del capacitor se abra cargado en un 57%, por lo que, el voltaje de la resistencia se abra descargado en dicho porcentaje. Entonces en un tiempo mayor a 4 segundos no abra voltaje en la resistencia ya que el capacitor estará completamente cargado.

 

vii.                Implemente el circuito R-C (figura 1) y con un osciloscopio observe y documente como el se comporta VR(t) cuando se aplica u(t)=5 V. Compárela con la obtenida en el punto iv. ¿Es la respuesta esperada? Justifique su respuesta y realice comentarios.

Nota: Debido a que no tenemos acceso a los laboratorios no podemos hacer esta parte de la experiencia.

viii.              Documente y describa la implementación y los resultados obtenidos.

 

b. Parte 2: Circuitos de orden superior

i.                     Halle de forma analítica la función de transferencia del circuito de la figura 2, tomando como señal de entrada Vin y como señal de salida Vout.

Figura 19. Circuito de orden superior hecho en Multisim

Si pasamos el circuito a Laplace podemos notar que solo cambian los condensadores debido a que la resistencia en Laplace es la misma resistencia , es decir:

Dividiremos el circuito en 4 partes por opamp , en este caso analizarimos:

·         Primer Opamp

Para el primer opamp de salida V0 podemos ver que tiene configuración conocida de amplificador en diferencia , entonces aplicando ley de kirchoff:

La razon del Vin/2 es que podemos ver un divisor de tencion para la patilla positiva donde las resistencias son iguales , por lo tanto la caída de tensión en cada uno es la mitad de la entrada.

·         Segundo Opamp

Para este opamp podemos ver un divisor de tensión también en la patilla positiva de U2 entre la resistencia R5 y el condensador C1 conr especto al voltaje de entrada que es VO1 entonces aplicando ley de kirchoff para determinar la salida del opamp VO2

 

·         Tercer Opamp

De la misma manera divisor de tensión en la patilla positiva

·         Cuarto Opamp

Aplicando ley de kirchoff deducimos

Reemplazando ec. 31 en ec. 30 ,posteriormente ec. 30 en ec. 29 finalmente ec. 29 en ec. 28

ii.                   Defina la función de transferencia en Matlab/Simulink y obtenga su respuesta temporal ante una entrada escalón e impulso unitario. Realice comentarios. 

Primeramente lo que haremos en matlab es definir nuestras constantes todo esto lo realizaremos en un Script , una vez definidos nuestras constantes tanto resistores y condensadores usamos nuestra función transferencia obtenida anteriormente y separamos 2 variables a modo vector entre corchetes , usando la función conv para el producto de los denominadores , una vez listo y definido el denominador y numerador usamos la función tf para obtener nuestra función de transferencia definida y lista para usarse en Simulink de la siguiente manera:

Figura 20.  Script para definir la función transferencia

Figura  21.  Resultado del Script

 

RESPUESTA DEL SISTEMA AL ESCALON

Una vez definido nuestra función transferencia vamos a poder utilizarlo en el Simulink por medio del bloque Tranfer. Function el cual como ya tenemos el numerador y el denominador en el workspace solo lo llamamos mediante las configuraciones del bloque como se muestra a continuación.

Figura 22.  Definiendo parámetros del bloque Transfer Fcn

 

Luego vamos a excitar nuestro sistema por medio del bloque step y para obtener la salida simplemente usamos el bloque scope.

Figura 23.  Modelado del sistema en Simulink

Figura 24.  Respuesta del sistema ante un escalón Simulink

 

Para visualizar la respuesta ante un step en Matlab , podremos hacerlo mediante el comando step(G) que nos resultara la siguiente grafica que necesariamente tiene que ser la misma que Simulink ya que son las mismas funciones de transferencia.

Figura 25.  Respuesta del sistema ante un escalón Matlab

 

RESPUESTA DEL SISTEMA AL IMPULSO UNITARIO

Para poder obtener la respuesta hacemos todo igual al anterior caso solo que esta vez lo excitaremos con un impulso que podemos lograr derivando nuestro escalón de la siguiente manera:

Figura 26.  Modelamiento del sistema Simulink

Figura 27. Respuesta del sistema ante un impulso Simulink

 

Para obtener la respuesta ante el impulso de una función transferencia necesitamos usar la función impulse(G) y nos dará un resultado igual que en Simulink.

Figura 28.  Respuesta ante un impulso Matlab

Análisis: como pudimos observar la grafica de la salida de nuestra función de transferencia cuando es excitada por el escalón unitario se estabiliza aproximadamente en un valor cercano entre 0.8 y 1 pero antes existe una valor mas alto que el punto en donde se estabiliza a comparación con el sistema excitado por un impulso el cual asciende rápidamente y luego decae hasta por debajo del valor cero pasando a negativo para luego estabilizarse en 0 cosa que tiene mucho sentido ya que la entra es un impulso que solamente existe en un punto de tiempo con una magnitud diferente de 0 en ese instante.

iii.                 Implemente el circuito propuesto en la figura 2 y con un osciloscopio observe y documente su respuesta temporal. Compárela con la obtenida en el punto ii. ¿Es la respuesta esperada? Justifique su respuesta y realice comentarios. 

La implementación se hizo en el software de Multisim usando el osciloscopio tectronix podemos ver la salida del circuito , para detectar la salida del circuito incorporamos al circuito un swicth en la entrada de voltaje , esto para cerrar el swicth podemos ver el comportamiento en ese instante en la salida de la siguiente manera:

Figura 29.  Respuesta del circuito en Multisim

 

De igual manera el circuito se implementó en el software de Proteus donde pudimos observar mejor el resultado acorde con lo obtenido anteriormente nuevamente incorporamos un swicth y lo accionamos para observar el camio en la salida:

Figura 30.  Respuesta del circuito en Proteus

Análisis: observamos que la respuesta en las simulaciones implementadas siguen un patrón bastante similar a la simulación en Matlab y Simulink , la señal de salida es mejor y mas evidente en el software de Proteus coincidiendo con lo obtenido y modelado teniendo como grafica una protuberancia antes de estabilizarse.

iv.                  Documente y describa la implementación y los resultados obtenidos. 

Como primera parte fue hallar la función de transferencia de nuestro circuito por medio del análisis de los opamps teniendo en cuenta que son ideales para facilitarnos el calculo , no sin antes pasar el circuito al dominio de Laplace en donde los únicos afectados serian los condensadores pero también los dominios respectivos de los voltajes al dominio de variable laplaciana S , una vez hecho esto se hizo análisis por partes , es decir a cada opamp se le hallo su salida relacionándolo con la entrada ya conocida , la reducción y análisis se hace sencilla si los opamps ideales tomábamos que las patillas tienen igual voltaje , además que la corriente que ingresa en sus terminales de entrada es igual a cero.

Una vez obtenida la función de transferencia en el dominio S en función de los resistores y condensadores podemos notar que el sistema converge y además que es de segundo orden , es decir que nuestro resultado tiene sentido por tanto podemos hacer la implementación matemática tanto del numerador como denominador en MATLAB , para lo cual Utilizamos las funciones conv (a,b) para producto de 2 funciones , la función tf(num,den) para expresar la función transferencia en base a numerador y denominador , finalmente ploteamos la expresión de transferencia excitándolo con un Step con su función respectiva , como también con la función impulse para obtener los resultados descritos.

Posteriormente la simulación del circuito en Proteus apoyándonos de un switch para producir el escalón en determinado instante y poder notar el cambio en el osciloscopio, obteniendo los resultados descritos en MATLAB.

 

III.     ANALISIS DE RESULTADOS

a.       En la figura 3, se presenta el clásico benchmark de 4 tanques propuesto por Johansson en [1].

Figura 31. Representación del Besmarch de 4 tanques

 

b.      Presente una descripción del funcionamiento del sistema.

Descripción del funcionamiento del sistema

El sistema de cuatro tanques acoplados por Johansson consiste en introducir un problema de control multivariable, el cual al linealizar el sistema cuenta con un cero multivariable que es posible se encuentre en el semiplano positivo o negativo. Este sistema esta compuesto por 4 tanques y dos bombas que se encuentran conectadas a dos válvulas de distribución del fluido. La bomba 1 suministra fluido del deposito inferior a los tanques 1 y 4 , los caudales que se dirigen a estos están regulados por la posición de la válvula 1 , esto es igual para los tanques 2 y 3 con la bomba 2  , además que la válvula 2 establece la cantidad de caudal.

Este sistema también cuenta con 2 sensores de nivel que se encuentran en los tanques 1 y 2 , estos se encargan de realizar la medición de los niveles de fluido. Otra cosa que podemos distinguir es que los tanques superiores o tanques 3 y 4 se descargan por los tanques 1 y 2 respectivamente y a su vez estos se descargan al depósito inferior, analizando el sistema podemos ver que existe relación en los tanques además de existir 2 entradas que son los voltajes aplicados a las bombas y 2 salidas que son los niveles de fluido, el cual hace un sistema multivariable.

Primero lo que hace el autor es hacer el modelo no lineal del sistema haciendo uso de la ecuación de balance de masas, el cual establece que la diferencia de la velocidad de entrada de masa en el sistema, debe ser igual a la diferencia de la velocidad de entrada de masa con la velocidad de salida de la misma.

Donde Ai es el área en [cm²] que es la sección transversal del tanque, hi [cm] es el nivel de agua, q_ini [cm³/s] es el flujo de entrada y q_outi es el flujo de salida, para i =1,2,3,4.

Entonces el flujo de entrada del tanque q_ini va a depender del voltaje aplicado en las bombas, aplicando las ecuaciones de bernoulii -torricelli se obtienen las ecuaciones no lineales del sistema de 4 tanques , de la siguiente manera:

·         Para el tanque 1:

Se nota claramente que existen 2 flujos entrantes que provienen del tanque 3 que se encuentra en la parte superior y contribuye con su flujo de salida, mientras que el otro aportante es la válvula que llega a la entrada del tanque uno , también existe un flujo de salida en el tanque 1 por ello la ecuación que describe el aporte de fluido estará determinado por:

 

·         Para el tanque 2:

Hacemos lo mismo que el tanque uno , haciendo una ecuación en base a  los aportantes de flujo respecto al tanque 2 , tanque 2 y tanque 4 aportan fujo mientras que el flujo escapa en la salida del tanque 2:

 

·         Para el tanque 3:

Para los tanques superiores se nota que el único aportante de flujo es por medio de la bomba 2 , y el flujo escapa en la salida del mismo tanque 3

·         Para el tanque 4:

Análogamente como el tanque 3 , este tanque solo tiene una entrada de flujo gestionado por la bomba 1 y unas salida de flujo en el mismo tanque 4

Entonces despejamos el cambio de la altura en el tiempo y las ecuaciones finales serian:

Figura 32. Se muestra todas las ecuaciones de diferencia generadas por el sistema

Luego de obtener las ecuaciones se procede a linealizar las expresiones haciendo uso de la serie de Taylor y la transformación de matriz jacobiana, posteriormente se evalúa y obtiene la matriz de función transferencia del sistema de 4 tanques para ello hallarla localización de los ceros , para interpretar las propiedades que puede tener y que influyen de diferente manera al sistema. La teoría de control identifica 2 tipos de sistema de acuerdo con la ubicación de sus ceros ya sea sistema de fase mínima , el cual todos sus ceros esta en el semiplano izquierdo (lo que implica parte real negativa) y sistema de fase no mínima , para lo cual al menos uno de sus ceros esta localizado en el semi plano derecho (parte real mayor que cero).

Las 2 matrices de transferencia para las condiciones de fase mínima y no mínima serán:

Figura 34. Matriz G

c.       Implemente su modelo en Simulink, puede utilizar los parámetros descritos en [1]

Figura 35. Se muestra el diagrama de bloques del sistema “clásico benchmark de 4 tanques”

 

Cuadro 1. Valores dados a los parámetros del sistema

Figura 36. Diagrama de bloques implementado con su forma gráfica

Figura 37. Para observar mejor el diagrama de bloques lo hemos dividido en 4 partes

 

Figura 38. Parte I:  Se muestra el tanque 1 y los diagramas de bloque que son su entrada 

Figura 39. Parte II:  Se muestra el tanque 2 y los diagramas de bloque que son su entrada

 

Figura 40. Parte III:  Se muestra el tanque 3 y los diagramas de bloque que son su entrada

 

Figura 41. Parte IV:  Se muestra el tanque 4 y los diagramas de bloque que son su entrada

Cuadro 1. Valores dados a los parámetros del sistema

Figura 42. Para observar mejor el diagrama de bloques en NMOP lo hemos dividido en 4 partes

Figura 43. Parte I:  Se muestra el tanque 1 y los diagramas de bloque que son su entrada

 

Figura 44. Parte II:  Se muestra el tanque 2 y los diagramas de bloque que son su entrada

Figura 45. Parte III:  Se muestra el tanque 3 y los diagramas de bloque que son su entrada

Figura 46. Parte IV:  Se muestra el tanque 4 y los diagramas de bloque que son su entrada

 

d.       Realice una simulación y analice si los resultados son los esperados.

Figura 47. Se muestra la configuración que tendrán los voltajes de entrada (u1 y u2)

MOP

Figura 48.  Diagrama de bloques del sistema 

Figura 49. Voltaje de entrada de u1(izquierda) y u2(derecha) 

Figura 50. Salida del tanque 1 – h1 (parte superior izquierda), del tanque 2 – h2 (parte superior derecha), tanque 3 – h3 (parte inferior izquierda) y del tanque 4 – h4 (parte inferior derecha) al tiempo de 10 segundos

Figura 51. Salida del tanque 1 – h1 (parte superior izquierda), del tanque 2 – h2 (parte superior derecha), tanque 3 – h3 (parte inferior izquierda) y del tanque 4 – h4 (parte inferior derecha) al tiempo de 200 segundos 

Figura 52. Salida del tanque 1 – h1 (parte superior izquierda), del tanque 2 – h2 (parte superior derecha), tanque 3 – h3 (parte inferior izquierda) y del tanque 4 – h4 (parte inferior derecha) al tiempo de 500 segundos

 

NMOP

Figura 53. Salida del tanque 1 – h1 (parte superior izquierda), del tanque 2 – h2 (parte superior derecha), tanque 3 – h3 (parte inferior izquierda) y del tanque 4 – h4 (parte inferior derecha) al tiempo de 10 segundos

Figura 54. Salida del tanque 1 – h1 (parte superior izquierda), del tanque 2 – h2 (parte superior derecha), tanque 3 – h3 (parte inferior izquierda) y del tanque 4 – h4 (parte inferior derecha) al tiempo de 200 segundos

Figura 55. Salida del tanque 1 – h1 (parte superior izquierda), del tanque 2 – h2 (parte superior derecha), tanque 3 – h3 (parte inferior izquierda) y del tanque 4 – h4 (parte inferior derecha) al tiempo de 500 segundos

 

IV.             CONCLUSIONES

·         El modelado del sistema requiere conocimientos físico matemáticos del modelo que se requiere modelar

·         Es posible hallar la función de transferencia por medio de un análisis matemático indicando las ecuaciones del cambio del sistema

·         Las ecuaciones que describen el comportamiento del sistema son útiles para modelar el sistema en el software de Simulink

·         Con Simulink podemos visualizar la respuesta de un determinado sistema ya sea al impulso o escalón que se trato en esta guía

·         Cabe destacar que la visualización de la respuesta también se puede hacer en matlab con el comando step(g) o impulse(g) donde g es la función transferencia del sistema

 

V.         REFERENCIAS BIBLIOGRAFICAS

 

ü  https://es.wikipedia.org/wiki/Funci%C3%B3n_escal%C3%B3n_de_Heaviside

ü  https://es.wikipedia.org/wiki/Funci%C3%B3n_rampa

ü  https://es.mathworks.com/help/simulink/slref/demux.html

ü  https://classroom.google.com/c/MTM0ODMyODAyNjIw/m/MTM3NTA1MTAwNDA2/details

ü  https://classroom.google.com/c/MTM0ODMyODAyNjIw/m/MTM3NTA1MTAwNDA2/details

ü  https://classroom.google.com/c/MTM0ODMyODAyNjIw/m/MTM3NTA1MTAwNDA2/details

ü  http://repository.udistrital.edu.co/bitstream/11349/13865/1/BernalRomeroJuanCarlos2018.pdf